
【题目】随机抽取某班6名学生,测量他们的身高(单位:cm),获得身高数据依次为:162,168,170,171,179,182,那么此班学生平均身高大约为cm;样本数据的方差为 .
【答案】172;45
【解析】解:计算数据:162,168,170,171,179,182的平均数为
![]() =
= ![]() ×(162+168+170+171+179+182)=172;
×(162+168+170+171+179+182)=172;
样本数据的方差为
s2= ![]() ×[(162﹣172)2+(168﹣172)2+(170﹣172)2+(171﹣172)2+(179﹣172)2+(182﹣172)2]=45,
×[(162﹣172)2+(168﹣172)2+(170﹣172)2+(171﹣172)2+(179﹣172)2+(182﹣172)2]=45,
所以答案是:172,45.
【考点精析】本题主要考查了平均数、中位数、众数和极差、方差与标准差的相关知识点,需要掌握⑴平均数、众数和中位数都是描述一组数据集中趋势的量;⑵平均数、众数和中位数都有单位;⑶平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以最为重要,应用最广;⑷中位数不受个别偏大或偏小数据的影响;⑸众数与各组数据出现的频数有关,不受个别数据的影响,有时是我们最为关心的数据;标准差和方差越大,数据的离散程度越大;标准差和方程为0时,样本各数据全相等,数据没有离散性;方差与原始数据单位不同,解决实际问题时,多采用标准差才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,点M是左侧面ADD1A1上的一个动点,满足 ![]()
![]() =1,则
=1,则 ![]() 与
与 ![]() 的夹角的最大值为( )
的夹角的最大值为( ) 
A.30°
B.45°
C.60°
D.75°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正四棱柱ABCD﹣A1B1C1D1中,AB=1,AA1=2,点P是平面A1B1C1D1内的一个动点,则三棱锥P﹣ABC的正视图与俯视图的面积之比的最大值为( ) 
A.1
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知P是抛物线y2=4x上的一个动点,则点P到直线l1:3x﹣4y+12=0和l2:x+2=0的距离之和的最小值是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下茎叶图记录了甲、乙两个篮球队在3次不同比赛中的得分情况.乙队记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以m表示.那么在3次比赛中,乙队平均得分超过甲队平均得分的概率是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+(2a+1)x+b,其中a,b∈R. (Ⅰ)当a=1,b=﹣4时,求函数f(x)的零点;
(Ⅱ)如果函数f(x)的图象在直线y=x+2的上方,证明:b>2;
(Ⅲ)当b=2时,解关于x的不等式f(x)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面ABC,底面三角形ABC是正三角形,E是BC中点,则下列叙述正确的是( )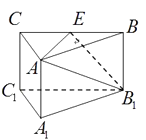
A.AC⊥平面ABB1A1
B.CC1与B1E是异面直线
C.A1C1∥B1E
D.AE⊥BB1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com