练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知直线上有一个动点，过点作直线垂直于轴，动点在上，且满足（为坐标原点），记点的轨迹为.

    （I）求曲线的方程；

    （II）若直线是曲线的一条切线，当点到直线的距离最短时，求直线的方程.

    【答案】（Ｉ）；（II）.

    【解析】试题分析：（I）设点，点，则由可得曲线的轨迹方程；（II）直线的斜率存在，设直线的方程为，联立曲线的方程，消去得， 可得，利用点到直线的距离公式和基本不等式求得时，点到直线的距离最短，此时，即可得直线的方程.

    试题解析：

    （I）设点，点，

    因为，所以，即，

    当时， 三点共线，不合题意，故，

    所以曲线的方程为；

    （II）直线与曲线相切，所以直线的斜率存在，

    设直线的方程为，

    由，得，

    直线与曲线相切，

    ，

    点到直线的距离

    ，

    当且仅当时等号成立，此时，

    所以直线的方程为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中， 底面，底面是直角梯形， ．

    （1）在上确定一点，使得平面，并求的值；

    （2）在（1）条件下，求平面与平面所成锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面，底面是直角梯形，．

    （1）在上确定一点，使得平面，并求的值；

    （2）在（1）条件下，求平面与平面所成锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    将圆上每一点的纵坐标保持不变，横坐标变为原来的2倍得到曲线．

    （1）写出曲线的参数方程；

    （2）以坐标原点为极点，轴正半轴为极轴坐标建立极坐标系，已知直线的极坐标方程为，若分别为曲线和直线上的一点，求的最近距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数的一段图象如图所示．

    (1)求函数的解析式；

    (2)将函数的图象向右平移个单位，得到的图象，求直线与

    函数的图象在内所有交点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】学校为测评班级学生对任课教师的满意度，采用“100分制”打分的方式来计分，规定满意度不低于98分，则评价该教师为“优秀”，现从某班学生中随机抽取10名，以下茎叶图记录了他们对某教师的满意度分数（以十位数字为茎，个位数字为叶）；

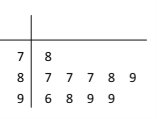
    （1）指出这组数据的众数和中位数；

    （2）求从这10人中随机选取3人，至多有1人评价该教师是“优秀”的概率；

    （3）以这10人的样本数据来估计整个班级的总体数据，若从该班任选3人，记表示抽到评价该教师为“优秀”的人数，求的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某省两相近重要城市之间人员交流频繁，为了缓解交通压力，特修一条专用铁路，用一列火车作为交通车，已知该车每次拖4节车厢，一日能来回16次，如果每次拖7节车厢，则每日能来回10次．

    （1）若每日来回的次数是车头每次拖挂车厢节数的一次函数，求此一次函数解析式：

    （2）在（1）的条件下，每节车厢能载乘客110人．问这列火车每天来回多少次才能使运营人数最多?并求出每天最多运营人数。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，二次函数，关于的不等式的解集为，其中为非零常数，设．

    （1）求的值；

    （2）若存在一条与轴垂直的直线和函数的图象相切，且切点的横坐标满足，求实数的取值范围；

    （3）当实数取何值时，函数存在极值？并求出相应的极值点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱中，点分别为线段的中点.

    （1）求证：平面；

    （2）若在边上，，求证：.

    查看答案和解析>>

    同步练习册答案