
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最小值;
上的最小值;
(2)若![]() ,求证:
,求证:![]() .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,圆形纸片的圆心为![]() ,半径为
,半径为![]() ,该纸片上的正方形
,该纸片上的正方形![]() 的中心为
的中心为![]() 为圆
为圆![]() 上的点,
上的点,![]() ,
,![]() ,
,![]() ,
,![]() 分别是以
分别是以![]() 为底边的等腰三角形.沿虚线剪开后,分别以
为底边的等腰三角形.沿虚线剪开后,分别以![]() 为折痕折起
为折痕折起![]() ,
,![]() ,
,![]() ,
,![]() 使得
使得![]() 重合,得到一个四棱锥.当该四棱锥的侧面积是底面积的2倍时,该四棱锥的外接球的表面积为__________.
重合,得到一个四棱锥.当该四棱锥的侧面积是底面积的2倍时,该四棱锥的外接球的表面积为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是椭圆
是椭圆![]() :
:![]() 上的两点,线段
上的两点,线段![]() 的中点在直线
的中点在直线![]() 上.
上.
(1)当直线![]() 的斜率
的斜率![]() 存在时,求实数
存在时,求实数![]() 的取值范围;
的取值范围;
(2)设![]() 是椭圆
是椭圆![]() 的左焦点,若椭圆
的左焦点,若椭圆![]() 上存在一点
上存在一点![]() ,使
,使![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,AB=2,AD=1.将矩形沿对角线BD折起,使A移到点P,P在平面BCD上的投影O恰好落在CD边上.
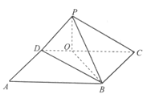
(1)证明:DP⊥平面BCP;
(2)求点O到平面PBD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年8月8日是我国第十个全民健身日,其主题是:新时代全民健身动起来。某市为了解全民健身情况,随机从某小区居民中抽取了40人,将他们的年龄分成7段:[10,20),[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图。

(1)试求这40人年龄的平均数、中位数的估计值;
(2)(i)若从样本中年龄在[50,70)的居民中任取2人赠送健身卡,求这2人中至少有1人年龄不低于60岁的概率;
(ⅱ)已知该小区年龄在[10,80]内的总人数为2000,若18岁以上(含18岁)为成年人,试估计该小区年龄不超过80岁的成年人人数。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两品牌计划入驻某商场,该商场批准两个品牌先进场试销![]() 天。两品牌提供的返利方案如下:甲品牌无固定返利,卖出
天。两品牌提供的返利方案如下:甲品牌无固定返利,卖出![]() 件以内(含
件以内(含![]() 件)的产品,每件产品返利
件)的产品,每件产品返利![]() 元,超出
元,超出![]() 件的部分每件返利
件的部分每件返利![]() 元;乙品牌每天固定返利
元;乙品牌每天固定返利![]() 元,且每卖出一件产品再返利
元,且每卖出一件产品再返利![]() 元。经统计,两家品牌在试销期间的销售件数的茎叶图如下:
元。经统计,两家品牌在试销期间的销售件数的茎叶图如下:
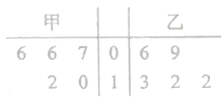
(Ⅰ)现从乙品牌试销的![]() 天中随机抽取
天中随机抽取![]() 天,求这
天,求这![]() 天的销售量中至少有一天低于
天的销售量中至少有一天低于![]() 的概率.
的概率.
(Ⅱ)若将频率视作概率,回答以下问题:
①记甲品牌的日返利额为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②商场拟在甲、乙两品牌中选择一个长期销售,如果仅从日返利额的角度考虑,请利用所学的统计学知识为商场作出选择,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com