
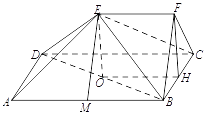
【题目】如图,在五面体 ![]() 中,四边形
中,四边形 ![]() 是边长为
是边长为 ![]() 的正方形,
的正方形, ![]() 平面
平面 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)求证: ![]() 平面
平面 ![]() ;
;
(2)求直线 ![]() 与平面
与平面 ![]() 所成角的正切值.
所成角的正切值.
【答案】
(1)证明:取 ![]() 的中点
的中点 ![]() ,连接
,连接 ![]() ,则
,则 ![]() ,
,
由(1)知, ![]() ,且
,且 ![]() ,
, ![]() 四边形
四边形 ![]() 为平行四边形,
为平行四边形,![]() ,
, ![]() ,
,
在 ![]() 中,
中, ![]() ,又
,又 ![]() ,得
,得 ![]() ,
, ![]() ,
,
在 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() ,即
,即 ![]() ,
,![]() 四边形
四边形 ![]() 是正方形,
是正方形, ![]() ,
,![]() ,
, ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]()
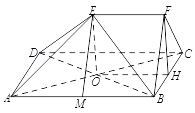
(2)解:解法1:连接 ![]() ,
, ![]() 与
与 ![]() 相交于点
相交于点 ![]() ,则点
,则点 ![]() 是
是 ![]() 的中点,
的中点,
取 ![]() 的中点
的中点 ![]() ,连接
,连接 ![]() 、
、 ![]() 、
、 ![]() ,
,
则 ![]() ,
, ![]() .
.
由(1)知 ![]() ,且
,且 ![]() ,
, ![]() ,且
,且 ![]() .
.![]() 四边形
四边形 ![]() 是平行四边形.
是平行四边形. ![]()
![]() ,且
,且 ![]() ,
,
由(1)知 ![]() 平面
平面 ![]() ,又
,又 ![]() 平面
平面 ![]() ,
, ![]() .
.![]() ,
, ![]() ,
, ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,
,![]() 平面
平面 ![]() .
. ![]() 平面
平面 ![]() .
.![]() 平面
平面 ![]() ,
, ![]() .
.![]() ,
, ![]() ,
, ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() .
.![]() 是直线
是直线 ![]() 与平面
与平面 ![]() 所成的角.
所成的角.
在 ![]() 中,
中, ![]() .
.![]() 直线
直线 ![]() 与平面
与平面 ![]() 所成角的正切值为
所成角的正切值为 ![]() ;
;
【解析】(1)根据题意作出辅助线利用平行四边形以及勾股定理可得出分别求出 E M、 F B的值,再利用勾股定理可得证A M ⊥ E M结合已知由线面垂直的判定定理可得证。(2)结合已知作出辅助线利用平行四边形和(1)的结论可得证FH⊥AB,由线面垂直的判定定理结合已知条件可得证E O ⊥ 平面 A B C D,再由线面垂直的性质定理可得出E O ⊥ A O ,进而找到直线AE在平面BDE上的射影故∠ A E O 是直线 A E 与平面 B D E 所成的角,借助解三角形的知识求出其值即可。


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xex+ax2+2x+1在x=﹣1处取得极值.
(1)求函数f(x)的单调区间;
(2)若函数y=f(x)﹣m﹣1在[﹣2,2]上恰有两个不同的零点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+ax2﹣ax,其中a∈R.
(1)当a=0时,求函数f(x)在x=1处的切线方程;
(2)若函数f(x)在定义域上有且仅有一个极值点,求实数a的取值范围;
(3)若对任意x∈[1,+∞),f(x)≥0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(4x+1)+kx与g(x)=log4(a2x﹣ ![]() a),其中f(x)是偶函数.
a),其中f(x)是偶函数.
(1)求实数k的值;
(2)求函数g(x)的定义域;
(3)若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E的右焦点与抛物线y2=4x的焦点重合,点M ![]() 在椭圆E上. (Ⅰ)求椭圆E的标准方程;
在椭圆E上. (Ⅰ)求椭圆E的标准方程;
(Ⅱ)设P(﹣4,0),直线y=kx+1与椭圆E交于A,B两点,若∠APO=∠BPO,(其中O为坐标原点),
求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示的平面图形中,ABCD是边长为2的正方形,△HDA和△GDC都是以D为直角顶点的等腰直角三角形,点E是线段GC的中点.现将△HDA和△GDC分别沿着DA,DC翻折,直到点H和G重合为点P.连接PB,得如图2的四棱锥. 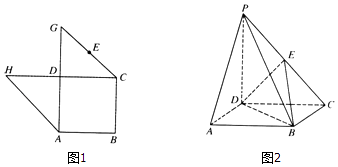
(Ⅰ)求证:PA∥平面EBD;
(Ⅱ)求二面角C﹣PB﹣D大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com