练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在△ABC中，三边a，c，b成等差，则sinA的范围是________．

    [）
    分析：利用等差数列的性质可知2c=a+b，利用余弦定理表示出cosC，然后把b=（a+c）代入，利用基本不等式即可求出cosC的最小值，根据C的范围及余弦函数在此区间为减函数即可得到A的范围，即可求
    解答：由三边成等差数列可知：c=
    由余弦定理得：cosC===≥=，
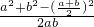
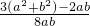
    当且仅当a=b时取等号，此时A=B
    又C∈（0，π），且余弦函数在此区间为减函数，
    所以C∈（0，]
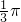
    所以，2A=A+B
    所以A∈，sinA∈[）
    故答案为：[）
    点评：此题考查学生灵活运用余弦定理化简求值，掌握余弦函数的图象与性质，灵活运用基本不等式求函数的最大值，是一道综合题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在△ABC中，三边a、b、c与面积S的关系是S=
    1
    4
    （a2+b2-c2），则角C应为（　　）
    A、30°B、45°
    C、60°D、90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，三边a、b、c所对的角分别为A、B、C，已知a=2
    		3
    ，b=2，△ABC的面积S=
    		3
    ，则C=
    π
    6
    或
    5π
    6
    π
    6
    或
    5π
    6
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，三边a，c，b成等差，则sinA的范围是
    [
    		3
    2
    ，1    ）
    [
    		3
    2
    ，1    ）
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，三边a、b、c与面积S的关系式为S=
    1
    4
    （a2+b2-c2），则角C=
    π
    4
    π
    4
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，三边a，b，c成等差数列，B=30°，三角形ABC的面积为
    1
    2
    ，则b的值是（　　）

    查看答案和解析>>

    同步练习册答案