
【题目】已知![]() .
.
(1)当a![]() 时,求证:
时,求证:![]() ;
;
(2)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值
上的最大值
【答案】(1)证明见解析;(2)ae2a﹣8a.
【解析】
(1)先求导,再根据导数和函数的最值即可求出,
(2)先求导,再分类讨论,当![]() 时,根据导数和函数的单调性即可而出,当
时,根据导数和函数的单调性即可而出,当![]() 时,可得
时,可得![]() 在
在![]() ,
,![]() 上的最大值为
上的最大值为![]() 和
和![]() 中的较大者,再构造函数比较,即可求出.
中的较大者,再构造函数比较,即可求出.
证明:(1)![]() 时,
时,![]() ,
,
![]() ,
,
令![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 单调递减,
单调递减,
![]() ,
,
即![]() ,问题得以证明;
,问题得以证明;
(2)![]() .
.![]() ,
,
![]() ,
,
令![]() ,解得
,解得![]() ,
,
①当![]() 时,
时,![]() ,即
,即![]() ,
,
![]() 在
在![]() ,
,![]() 上单调递增,
上单调递增,
![]() ;
;
②当![]() 时,
时,![]() ,
,
设![]() ,
,
所以![]() ,即
,即![]() 在
在![]() ,
,![]() 上单调递增,
上单调递增,
![]() ,即
,即![]() ,
,
![]() ,
,
![]() 当
当![]() ,
,![]() 时,
时,![]() ,即
,即![]() 单调递减,
单调递减,
当![]() ,
,![]() 时,
时,![]() ,即
,即![]() 单调递增,
单调递增,
![]() 在
在![]() ,
,![]() 上的最大值为
上的最大值为![]() 和
和![]() 中的较大者,
中的较大者,
![]() ,
,
设![]() ,则
,则![]() 在
在![]() 上恒小于0,
上恒小于0,
![]() ,即
,即![]() ,
,
![]()
![]() ,
,![]() ,
,
![]() ,
,
![]() 在
在![]() ,
,![]() 上的最大值为
上的最大值为![]() ;
;
综上所述函数![]() 在
在![]() ,
,![]() 上的最大值
上的最大值![]() .
.


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为![]() (t为参数),在以直角坐标系的原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为
(t为参数),在以直角坐标系的原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为![]()
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)若直线l与曲线C相交于A,B两点,求△AOB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣a(x2+x+1).
(1)当a=1时,证明:f(x)+x2≥0;
(2)当a![]() 时,判断函数f(x)的单调性;
时,判断函数f(x)的单调性;
(3)若函数f(x)有三个零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近期,济南公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用![]() 表示活动推出的天数,
表示活动推出的天数, ![]() 表示每天使用扫码支付的人次(单位:十人次),统计数据如表
表示每天使用扫码支付的人次(单位:十人次),统计数据如表![]() 所示:
所示:

根据以上数据,绘制了散点图.

(1)根据散点图判断,在推广期内, ![]() 与
与![]() (
(![]() 均为大于零的常数)哪一个适宜作为扫码支付的人次
均为大于零的常数)哪一个适宜作为扫码支付的人次![]() 关于活动推出天数
关于活动推出天数![]() 的回归方程类型?(给出判断即可,不必说明理由);
的回归方程类型?(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表![]() 中的数据,建立
中的数据,建立![]() 关于
关于![]() 的回归方程,并预测活动推出第
的回归方程,并预测活动推出第![]() 天使用扫码支付的 人次;
天使用扫码支付的 人次;
(3)推广期结束后,车队对乘客的支付方式进行统计,结果如下

车队为缓解周边居民出行压力,以![]() 万元的单价购进了一批新车,根据以往的经验可知,每辆车每个月的运营成本约为
万元的单价购进了一批新车,根据以往的经验可知,每辆车每个月的运营成本约为![]() 万元.已知该线路公交车票价为
万元.已知该线路公交车票价为![]() 元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受
元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受![]() 折优惠,扫码支付的乘客随机优惠,根据统计结果得知,使用扫码支付的乘客中有
折优惠,扫码支付的乘客随机优惠,根据统计结果得知,使用扫码支付的乘客中有![]() 的概率享受
的概率享受![]() 折优惠,有
折优惠,有![]() 的概率享受
的概率享受![]() 折优惠,有
折优惠,有![]() 的概率享受
的概率享受![]() 折优惠.预计该车队每辆车每个月有
折优惠.预计该车队每辆车每个月有![]() 万人次乘车,根据给数据以事件发生的频率作为相应事件发生的概率,在不考虑其它因素的条件下,按照上述收费标准,假设这批车需要
万人次乘车,根据给数据以事件发生的频率作为相应事件发生的概率,在不考虑其它因素的条件下,按照上述收费标准,假设这批车需要![]() 年才能开始盈利,求
年才能开始盈利,求![]() 的值.
的值.
参考数据:

其中其中![]()
参考公式:
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: 
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,抛物线
,抛物线![]() 与圆
与圆![]() 的相交弦长为4.
的相交弦长为4.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)点![]() 为抛物线
为抛物线![]() 的焦点,
的焦点,![]() 为抛物线
为抛物线![]() 上两点,
上两点,![]() ,若
,若![]() 的面积为
的面积为![]() ,且直线
,且直线![]() 的斜率存在,求直线
的斜率存在,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水产养殖户在鱼成熟时,随机从网箱中捕捞100尾鱼,其质量分别在[4,4.5),[4.5.5),[5.5.5),[5.5,6),[6,6.5),[6.5,7](单位:斤)中,经统计得频率分布直方图如图所示
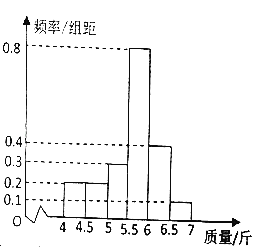
(1)现按分层抽样的方法,从质量为[4.5,5),[5,5.5)的鱼中随机抽取5尾,再从这5尾中随机抽取2尾,记随机变量X表示质量在[4.5,5)内的鱼的尾数,求X的分布列及数学期望.
(2)以各组数据的中间数代表这组数据的平均值,将频率视为概率,该养殖户还未捕捞的鱼大约还有1000尾,现有两个方案:
方案一:所有剩余的鱼现在卖出,质量低于5.5斤的鱼售价为每斤10元,质量高于5.5斤的鱼售价为每斤12元
方案二:一周后所有剩余的鱼逢节日卖出,假设每尾鱼的质量不变,鱼的数目不变,质量低于5.5斤的鱼售价为每斤15元,这类鱼养殖一周的费用是平均每尾22元;质量高于5.5斤的鱼售价为每斤16元,这类鱼养殖一周的费用是平均每尾24元通过计算确定水产养殖户选择哪种方案获利更多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com