
°æƒø°øπ≤œÌµ•≥µµƒÕ∆π„∏¯œ˚∑—’þ¥¯¿¥»´–¬œ˚∑—×ȣ¨—∏ÀŸ”Ƶ√π„¥Ûœ˚∑—’þµƒ«ýÌ˘£¨»ª∂¯£¨Õ¨ ±“≤±©¬∂≥ˆπп̰¢Õ£∑≈°¢∑˛ŒÒµ»∑Ω√ʵƒŒ £¨Œ™¡À¡ÀΩ‚π´÷⁄∂‘π≤œÌµ•≥µµƒÃ¨∂»£®Ã·≥´ªÚ≤ªÃ·≥´£©£¨ƒ≥µ˜≤È–°◊ÈÀʪ˙µÿ∂‘≤ªÕ¨ƒÍ¡‰∂Œ50»ÀΩ¯––µ˜≤È£¨Ω´µ˜≤È«Èøˆ’˚¿Ì»Áœ¬±Ì£∫

≤¢«“£¨ƒÍ¡‰‘⁄![]() ∫Õ
∫Õ![]() µƒ»À÷–≥÷°∞÷≥´°±Ã¨∂»µƒ»À ˝∑÷±Œ™5∫Õ3£¨œ÷¥”’‚¡Ω∏ˆƒÍ¡‰∂Œ÷–Àʪ˙≥È»°2»À’˜«Û“‚º˚.
µƒ»À÷–≥÷°∞÷≥´°±Ã¨∂»µƒ»À ˝∑÷±Œ™5∫Õ3£¨œ÷¥”’‚¡Ω∏ˆƒÍ¡‰∂Œ÷–Àʪ˙≥È»°2»À’˜«Û“‚º˚.
£®¢Ò£©«ÛƒÍ¡‰‘⁄![]() ÷–±ª≥ÈµΩµƒ2»À∂º≥÷°∞÷≥´°±Ã¨∂»µƒ∏≈¬ £ª
÷–±ª≥ÈµΩµƒ2»À∂º≥÷°∞÷≥´°±Ã¨∂»µƒ∏≈¬ £ª
£®¢Ú£©«ÛƒÍ¡‰‘⁄![]() ÷–±ª≥ÈµΩµƒ2»À÷¡…Ÿ1»À≥÷°∞÷≥´°±Ã¨∂»µƒ∏≈¬ .
÷–±ª≥ÈµΩµƒ2»À÷¡…Ÿ1»À≥÷°∞÷≥´°±Ã¨∂»µƒ∏≈¬ .
°æ¥∞∏°ø£®1£©![]() £ª£®2£©
£ª£®2£©![]() .
.
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©ƒÍ¡‰‘⁄[20£¨25£©÷–π≤”–6»À£¨∆‰÷–≥÷°∞÷≥´°±Ã¨∂»µƒ»À ˝Œ™5£¨∆‰÷–≥È¡Ω»À£¨ª˘±æ ¬º˛◊Ð ˝n=15£¨±ª≥ÈµΩµƒ2»À∂º≥÷°∞÷≥´°±Ã¨∂»∞¸∫¨µƒª˘±æ ¬º˛∏ˆ ˝m=10£¨”…¥ÀƒÐ«Û≥ˆƒÍ¡‰‘⁄[20£¨25£©÷–±ª≥ÈµΩµƒ2»À∂º≥÷°∞÷≥´°±Ã¨∂»µƒ∏≈¬ £Æ£®2£©ƒÍ¡‰‘⁄[40£¨45£©÷–π≤”–5»À£¨∆‰÷–≥÷°∞÷≥´°±Ã¨∂»µƒ»À ˝Œ™3£¨∆‰÷–≥È¡Ω»À£¨ª˘±æ ¬º˛◊Ð ˝n°‰=10£¨ƒÍ¡‰‘⁄[40£¨45£©÷–±ª≥ÈµΩµƒ2»À÷¡…Ÿ1»À≥÷°∞÷≥´°±Ã¨∂»∞¸∫¨µƒª˘±æ ¬º˛∏ˆ ˝m°‰=9£¨”…¥ÀƒÐ«Û≥ˆƒÍ¡‰‘⁄[40£¨45£©÷–±ª≥ÈµΩµƒ2»À÷¡…Ÿ1»À≥÷°∞÷≥´°±Ã¨∂»µƒ∏≈¬ £Æ
Ω‚Œˆ£∫
£®1£©…Ë‘⁄![]() ÷–µƒ6»À≥÷°∞÷≥´°±Ã¨∂»µƒŒ™
÷–µƒ6»À≥÷°∞÷≥´°±Ã¨∂»µƒŒ™![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨≥÷°∞≤ªÃ·≥´°±Ã¨∂»µƒŒ™
£¨≥÷°∞≤ªÃ·≥´°±Ã¨∂»µƒŒ™![]() .
.
◊еƒª˘±æ ¬º˛”–£®![]() £©£¨£®
£©£¨£®![]() £©£¨£®
£©£¨£®![]() £©£¨£®
£©£¨£®![]() £©£¨£®
£©£¨£®![]() £©£¨£®
£©£¨£®![]() £©£¨£®
£©£¨£®![]() £©£¨£®
£©£¨£®![]() £©£¨£®
£©£¨£®![]() £©£¨£®
£©£¨£®![]() £©£¨£®
£©£¨£®![]() £©£¨£®
£©£¨£®![]() £©£¨£®
£©£¨£®![]() £©£¨£®
£©£¨£®![]() £©£¨£®
£©£¨£®![]() £©.π≤15∏ˆ£¨∆‰÷–¡Ω»À∂º≥÷°∞÷≥´°±Ã¨∂»µƒ”–10∏ˆ£¨
£©.π≤15∏ˆ£¨∆‰÷–¡Ω»À∂º≥÷°∞÷≥´°±Ã¨∂»µƒ”–10∏ˆ£¨
À˘“‘P=![]() =
=![]()
£®2£©…Ë‘⁄![]() ÷–µƒ5»À≥÷°∞÷≥´°±Ã¨∂»µƒŒ™
÷–µƒ5»À≥÷°∞÷≥´°±Ã¨∂»µƒŒ™![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨≥÷°∞≤ªÃ·≥´°±Ã¨∂»µƒŒ™
£¨≥÷°∞≤ªÃ·≥´°±Ã¨∂»µƒŒ™![]() £¨
£¨ ![]() .
.
◊еƒª˘±æ ¬º˛”–(![]() )£¨(
)£¨(![]() )£¨(
)£¨(![]() )£¨(
)£¨(![]() )£¨(
)£¨(![]() )£¨(
)£¨(![]() )£¨(
)£¨(![]() )£¨(
)£¨(![]() )£¨(
)£¨(![]() )£¨(
)£¨(![]() )£¨π≤10∏ˆ£¨∆‰÷–¡Ω»À∂º≥÷°∞≤ªÃ·≥´°±Ã¨∂»µƒ÷ª”–(
)£¨π≤10∏ˆ£¨∆‰÷–¡Ω»À∂º≥÷°∞≤ªÃ·≥´°±Ã¨∂»µƒ÷ª”–(![]() )“ª÷÷£¨À˘“‘P=
)“ª÷÷£¨À˘“‘P=![]() =
=![]()



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™![]() «
«![]() ƒ⁄Ω«
ƒ⁄Ω«![]() µƒΩ«∆Ω∑÷œþ.
µƒΩ«∆Ω∑÷œþ.

£®1£©”√’˝œ“∂®¿Ì÷§√˜£∫ ![]() £ª
£ª
£®2£©»Ù![]() £¨«Û
£¨«Û![]() µƒ≥§.
µƒ≥§.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤![]() æ≠π˝µ„M£®©Å2£¨©Å1£©£¨¿Î–ƒ¬ Œ™
æ≠π˝µ„M£®©Å2£¨©Å1£©£¨¿Î–ƒ¬ Œ™![]() £Æπ˝µ„M◊˜«„–±Ω«ª•≤πµƒ¡ΩÃı÷±œþ∑÷±”ÎÕ÷‘≤CΩª”⁄“Ï”⁄Mµƒ¡ÌÕ‚¡Ωµ„P°¢Q£Æ
£Æπ˝µ„M◊˜«„–±Ω«ª•≤πµƒ¡ΩÃı÷±œþ∑÷±”ÎÕ÷‘≤CΩª”⁄“Ï”⁄Mµƒ¡ÌÕ‚¡Ωµ„P°¢Q£Æ
(¢Ò)«ÛÕ÷‘≤Cµƒ∑Ω≥ãª
£®¢Ú£© ‘≈–∂œ÷±œþPQµƒ–±¬ «∑ÒŒ™∂®÷µ£¨÷§√˜ƒ„µƒΩ·¬€£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº,Àƒ¿‚◊∂![]() ÷–,
÷–, ![]() Œ™’˝»˝Ω«–Œ,
Œ™’˝»˝Ω«–Œ, ![]() ,
, ![]() Œ™¿‚
Œ™¿‚![]() µƒ÷–µ„.
µƒ÷–µ„.
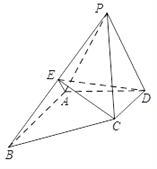
(1)«Û÷§:∆Ω√Ê![]() ∆Ω√Ê
∆Ω√Ê![]() ;
;
(2)»Ù÷±œþ![]() ”Î∆Ω√Ê
”Î∆Ω√Ê![]() À˘≥…Ω«Œ™
À˘≥…Ω«Œ™![]() ,«Û∂˛√ÊΩ«
,«Û∂˛√ÊΩ«![]() µƒ”ýœ“÷µ.
µƒ”ýœ“÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() .
.
£®1£©Ã÷¬€![]() µƒµ•µ˜«¯º‰£ª
µƒµ•µ˜«¯º‰£ª
£®2£©µ±![]() ±£¨÷§√˜£∫
±£¨÷§√˜£∫ ![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø£®ƒ≥±£œ’π´Àæ”–“ªøÓ±£œ’≤˙∆∑µƒ¿˙ ∑ªßªÒ“ʬ £®ªÒ“ʬ =ªÒ“Ê°¬±£∑— ’»Î£©µƒ∆µ¬ ∑÷≤º÷±∑ΩÕº»ÁÕºÀ˘ æ£∫
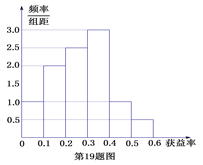
£®¢Ò£© ‘π¿º∆∆Ωæ˘ ’“ʬ £ª
£®¢Ú£©∏˘æðæ≠—È»Ù√ø∑ð±£µ•µƒ±£∑—‘⁄![]() ‘™µƒª˘¥°…œ√ø‘ˆº”
‘™µƒª˘¥°…œ√ø‘ˆº”![]() ‘™£¨∂‘”¶µƒœ˙¡ø
‘™£¨∂‘”¶µƒœ˙¡ø![]() £®ÕÚ∑𣩔Î
£®ÕÚ∑𣩔Î![]() £®‘™£©”–Ωœ«øœþ–‘œýπÿπÿœµ£¨¥”¿˙ ∑œ˙ €º«¬º÷–≥È—˘µ√µΩ»Áœ¬
£®‘™£©”–Ωœ«øœþ–‘œýπÿπÿœµ£¨¥”¿˙ ∑œ˙ €º«¬º÷–≥È—˘µ√µΩ»Áœ¬![]() ◊È
◊È![]() ”Î
”Î![]() µƒ∂‘”¶ ˝æð£∫
µƒ∂‘”¶ ˝æð£∫
|
|
|
|
|
|
œ˙¡ø |
|
|
|
|
|
£®¢°£©∏˘æð ˝æðº∆À„≥ˆœ˙¡ø![]() £®ÕÚ∑𣩔Î
£®ÕÚ∑𣩔Î![]() £®‘™£©µƒªÿπÈ∑Ω≥ÃŒ™
£®‘™£©µƒªÿπÈ∑Ω≥ÃŒ™![]() £ª
£ª
£®¢¢£©»Ù∞—ªÿπÈ∑Ω≥Ã![]() µ±◊˜
µ±◊˜![]() ”Î
”Î![]() µƒœþ–‘πÿœµ£¨”√£®¢Ò£©÷–«Û≥ˆµƒ∆Ωæ˘ªÒ“Ê¬ π¿º∆¥À≤˙∆∑µƒªÒ“ʬ £¨√ø∑ð±£µ•µƒ±£∑—∂®Œ™∂ý…Ÿ‘™ ±¥À≤˙∆∑ø…ªÒµ√◊Ó¥ÛªÒ“Ê£¨≤¢«Û≥ˆ∏√◊Ó¥ÛªÒ“Ê.
µƒœþ–‘πÿœµ£¨”√£®¢Ò£©÷–«Û≥ˆµƒ∆Ωæ˘ªÒ“Ê¬ π¿º∆¥À≤˙∆∑µƒªÒ“ʬ £¨√ø∑ð±£µ•µƒ±£∑—∂®Œ™∂ý…Ÿ‘™ ±¥À≤˙∆∑ø…ªÒµ√◊Ó¥ÛªÒ“Ê£¨≤¢«Û≥ˆ∏√◊Ó¥ÛªÒ“Ê.
≤Œøºπ´ æ£∫ 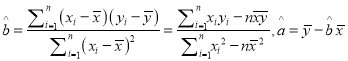
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™»˝¿‚÷˘![]() ÷–£¨
÷–£¨ ![]() ∆Ω√Ê
∆Ω√Ê![]() £¨
£¨ ![]() £¨
£¨ ![]() ∑÷± «¿‚
∑÷± «¿‚![]() µƒ÷–µ„.
µƒ÷–µ„.
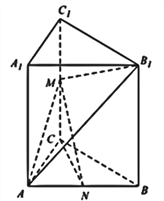
£®1£©«Û÷§£∫ ![]() ∆Ω√Ê
∆Ω√Ê![]() £ª
£ª
£®2£©«Û÷§£∫ ![]() ∆Ω√Ê
∆Ω√Ê![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øπ©µÁ≤ø√≈∂‘ƒ≥…Á«¯![]() Œªæ”√Ò2016ƒÍ11‘¬∑ð»Àæ˘”√µÁ«ÈøˆΩ¯––Õ≥º∆∫Û£¨∞¥»Àæ˘”√µÁ¡ø∑÷Œ™
Œªæ”√Ò2016ƒÍ11‘¬∑ð»Àæ˘”√µÁ«ÈøˆΩ¯––Õ≥º∆∫Û£¨∞¥»Àæ˘”√µÁ¡ø∑÷Œ™![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨
£¨ ![]() ŒÂ◊È£¨’˚¿Ìµ√µΩ»Áœ¬µƒ∆µ¬ ∑÷≤º÷±∑ΩÕº£¨‘Úœ¬¡–Àµ∑®¥ÌŒÛµƒ «£® £©
ŒÂ◊È£¨’˚¿Ìµ√µΩ»Áœ¬µƒ∆µ¬ ∑÷≤º÷±∑ΩÕº£¨‘Úœ¬¡–Àµ∑®¥ÌŒÛµƒ «£® £©
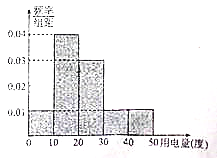
A. 11‘¬∑ð»Àæ˘”√µÁ¡ø»À ˝◊Ó∂ýµƒ“ª◊È”–![]() »À
»À
B. 11‘¬∑ð»Àæ˘”√µÁ¡ø≤ªµÕ”⁄![]() ∂»µƒ”–
∂»µƒ”–![]() »À
»À
C. 11‘¬∑ð»Àæ˘”√µÁ¡øŒ™![]() ∂»
∂»
D. ‘⁄’‚![]() Œªæ”√Ò÷–»Œ—°
Œªæ”√Ò÷–»Œ—°![]() Œª–≠÷˙ ’∑—£¨—°µΩµƒæ”√Ò”√µÁ¡ø‘⁄
Œª–≠÷˙ ’∑—£¨—°µΩµƒæ”√Ò”√µÁ¡ø‘⁄![]() “ª◊ȵƒ∏≈¬ Œ™
“ª◊ȵƒ∏≈¬ Œ™![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™![]() £¨∆‰÷–≥£ ˝
£¨∆‰÷–≥£ ˝![]() .
.
£®1£©µ±![]() ±£¨«Û∫Ø ˝
±£¨«Û∫Ø ˝![]() µƒº´÷µ£ª
µƒº´÷µ£ª
£®2£©»Ù∫Ø ˝![]() ”–¡Ω∏ˆ¡„µ„
”–¡Ω∏ˆ¡„µ„![]() £¨«Û÷§£∫
£¨«Û÷§£∫ ![]() £ª
£ª
£®3£©«Û÷§£∫ ![]() .
.
—°◊ˆÃ‚£∫
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com