
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的极值;
的极值;
(2)若函数![]() 的图象恒在直线
的图象恒在直线![]() 的下方.
的下方.
①求实数![]() 的取值范围;
的取值范围;
②求证:对任意正整数![]() ,都有
,都有![]() .
.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数).在以
为参数).在以![]() 为极点、
为极点、![]() 轴的非负半轴为极轴的极坐标系(两种坐标系的单位长度相同)中,曲线
轴的非负半轴为极轴的极坐标系(两种坐标系的单位长度相同)中,曲线![]() :
:![]() 的焦点
的焦点![]() 的极坐标为
的极坐标为![]() .
.
(1)求常数![]() 的值;
的值;
(2)设![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() ,求
,求![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和Sn满足2Sn=an+2﹣2,n∈N*.
(1)若数列{an}为等比数列,求数列{an}的公比q的值.
(2)若a2=a1=1,bn=an+an+1,求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
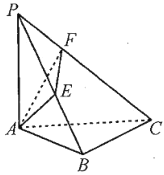
【题目】在《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑.如图,在鳖臑![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,过点
,过点![]() 分别作
分别作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连结
,连结![]() ,当
,当![]() 的面积最大值时,
的面积最大值时,![]() ( ).
( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
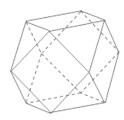
【题目】半正多面体亦称“阿基米德多面体”,是由边数不全相同的正多边形为面的多面体,体现了数学的对称美.如图,将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,如此共可截去八个三棱锥,得到一个有十四个面的半正多面体,它们的棱长都相等,其中八个为正三角形,六个为正方形,称这样的半正多面体为二十四等边体.若棱长为![]() 的二十四等边体的各个顶点都在同一个球面上,则该球的表面积为( )
的二十四等边体的各个顶点都在同一个球面上,则该球的表面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为进行爱国主义教育,在全校组织了一次有关钓鱼岛历史知识的竞赛.现有甲、乙两队参加钓鱼岛知识竞赛,每队3人,规定每人回答一个问题,答对为本队赢得1分,答错得0分.假设甲队中每人答对的概率均为![]() ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为![]() ,且各人回答正确与否相互之间没有影响,用ξ表示甲队的总得分.
,且各人回答正确与否相互之间没有影响,用ξ表示甲队的总得分.
(Ⅰ)求随机变量ξ的分布列和数学期望;
(Ⅱ)用![]() 表示“甲、乙两个队总得分之和等于3”这一事件,用
表示“甲、乙两个队总得分之和等于3”这一事件,用![]() 表示“甲队总得分大于乙队总得分” 这一事件,求
表示“甲队总得分大于乙队总得分” 这一事件,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com