练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

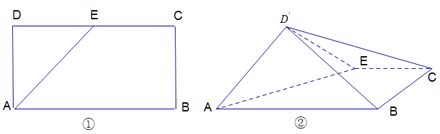
    【题目】如图①，在矩形中， ， 是的中点，将三角形沿翻折到图②的位置，使得平面平面.

    (Ⅰ)在线段上确定点，使得平面，并证明；

    (Ⅱ)求与所在平面构成的锐二面角的正切值.

    【答案】（1）点是线段中点时， 平面，证明见解析；（2）.

    【解析】试题分析：(Ⅰ) ， 的延长线交于点，由已知可得点是的中点，取BD的中点，由三角形的中位线可得，可证；（2）由条件可得，进而可得 平面.在平面内作 ，由线面垂直的性质可得 .所以就是与所在平面构成的锐二面角的平面角.求角即可。

    试题解析：(Ⅰ)点是线段中点时， 平面.

    证明：记， 的延长线交于点，因为，所以点是的中点，

    所以.

    而在平面内， 在平面外，

    所以平面.

    (Ⅱ)在矩形中， ， ，

    因为平面 平面，且交线是，

    所以 平面.

    在平面内作 ，连接，

    则 .

    所以就是与所在平面构成的锐

    二面角的平面角.

    因为, ，

    所以.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

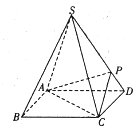
    【题目】如图，四棱锥的底面是正方形，每条侧棱的长都是底面边长的倍，P为侧棱SD上的点，且.

    （1）求二面角的大小；

    （2）在侧棱SC上是否存在一点E，使得平面？若存在，求 的值；若不存在，试说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数， （）．

    （Ⅰ）求函数的单调区间；

    （Ⅱ）若函数在处取得极大值，求正实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆过， 两点，且圆心在直线上.

    （1）求圆的方程；

    （2）若直线过点且被圆截得的线段长为，求的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在某次测试后，一位老师从本班48同学中随机抽取6位同学，他们的语文、历史成绩如下表：

    学生编号

    1

    2

    3

    4

    5

    6

    语文成绩

    60

    70

    74

    90

    94

    110

    历史成绩

    58

    63

    75

    79

    81

    88

    (1)若规定语文成绩不低于90分为优秀，历史成绩不低于80分为优秀，以频率作概率，分别估计该班语文、历史成绩优秀的人数；

    (2)用上表数据画出散点图易发现历史成绩与语文成绩具有较强的线性相关关系，求与的线性回归方程（系数精确到0.1）.

    参考公式：回归直线方程是，其中，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在三角形ABC中，分别根据下列条件解三角形，其中有两个解的是（ ）
    A.a=8b=16A=30°
    B.a=25b=30A=150°
    C.a=30b=40A=30°
    D.a=72b=60A=135°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线上的点到点的距离比它到直线的距离小2.

    （1）求曲线的方程；

    （2）过点且斜率为的直线交曲线于， 两点，若，当时，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

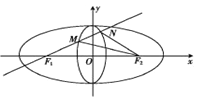
    【题目】定义：若两个椭圆的离心率相等，则称两个椭圆是“相似”的.如图，椭圆与椭圆是相似的两个椭圆，并且相交于上下两个顶点.椭圆的长轴长是4，椭圆短轴长是1，点分别是椭圆的左焦点与右焦点.

    （1）求椭圆的方程；

    （2）过的直线交椭圆于点，求面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在正方体ABCD﹣A1B1C1D1中，E、F分别为棱AB、AD的中点．
    （1）求证：EF平行平面CB1D1；
    （2）求证：平面CAA1C1⊥平面CB1D1
    （3）求直线A1C与平面ABCD所成角的正切值．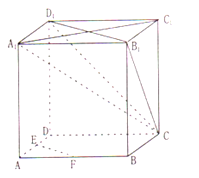

    查看答案和解析>>

    同步练习册答案