Question

【题目】已知椭圆C： =1（a＞b＞0）的右焦点为（ ，0），离心率为 ．
（1）求椭圆C的标准方程；
（2）若动点P（x0 ， y0）为椭圆C外一点，且点P到椭圆C的两条切线相互垂直，求点P的轨迹方程．

Answer 1

【答案】
（1）解：依题意知 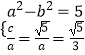，求得a=3，b=2，

∴椭圆的方程为 =1

（2）解：①当两条切线中有一条斜率不存在时，即A、B两点分别位于椭圆长轴与短轴的端点，P的坐标为（±3，±2），符合题意，

②当两条切线斜率均存在时，设过点P（x0，y0）的切线为y=k（x﹣x0）+y0，

= + =1，整理得（9k2+4）x2+18k（y0﹣kx0）x+9[（y0﹣kx0）2﹣4]=0，

∴△=[18k（y0﹣kx0）]2﹣4（9k2+4）×9[（y0﹣kx0）2﹣4]=0，

整理得（x02﹣9）k2﹣2x0×y0×k+（y02﹣4）=0，

∴﹣1=k1k2= =﹣1，

∴x02+y02=13．

把点（±3，±2）代入亦成立，

∴点P的轨迹方程为：x2+y2=13

【解析】（1）根据焦点坐标和离心率求得a和b，则椭圆的方可得．（2）设出切线的方程，带入椭圆方程，整理后利用△=0，整理出关于k的一元二次方程，利用韦达定理表示出k1k2 ， 进而取得x0和y0的关系式，即P点的轨迹方程．
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识，掌握椭圆标准方程焦点在x轴：，焦点在y轴：．