练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知双曲线:的左、右焦点分别为、，为坐标原点，是双曲线在第一象限上的点，直线交双曲线左支于点，直线 交双曲线右支于点，若，且，则双曲线的渐近线方程为（ ）

    A. B. C. D.

    【答案】A

    【解析】

    由题意，根据双曲线的定义和余弦定理，可得a与c的关系，再求出a与b关系即可求出渐近线方程.

    解：由题意，|PF1|＝2|PF2|，|PF1|﹣|PF2|＝2a，

    ∴|PF1|＝4a，|PF2|＝2a，

    由于P,M关于原点对称， 关于原点对称，所以线段 , 互相平分，

    四边形 为平行四边形， ,

    ∵∠MF2N＝60°，

    ∴∠F1PF2＝60°，

    由余弦定理可得4c2＝16a2+4a2﹣24a2acos60°，

    ∴c＝a，

    ∴b＝＝a．

    ∴ ，

    ∴双曲线C的渐近线方程为y＝±x

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知抛物线：.

    （Ⅰ）、是抛物线上不同于顶点的两点，若以为直径的圆经过抛物线的顶点，试证明直线必过定点，并求出该定点的坐标；

    （Ⅱ）在（Ⅰ）的条件下，抛物线在、处的切线相交于点，求面积的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的图象如图所示，令，则下列关于函数的说法中不正确的是（ ）

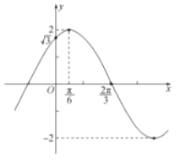
    A. 函数图象的对称轴方程为

    B. 函数的最大值为

    C. 函数的图象上存在点，使得在点处的切线与直线：平行

    D. 方程的两个不同的解分别为，，则最小值为

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的图象上存在点，函数的图象上存在点，且，关于轴对称，则的取值范围是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国明代珠算家程大位的名著《直指算法统宗》中有如下问题：“今有白米一百八十石，令三人从上及和减率分之，只云甲多丙米三十六石，问：各该若干？”其意思为：“今有白米一百八十石，甲、乙、丙三人来分，他们分得的白米数构成等差数列，只知道甲比丙多分三十六石，那么三人各分得多少白米？”请问：乙应该分得（ ）白米

    A. 96石B. 78石C. 60石D. 42石

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某乐园按时段收费，收费标准为：每玩一次不超过小时收费10元，超过小时的部分每小时收费元（不足小时的部分按小时计算）．现有甲、乙二人参与但都不超过小时，甲、乙二人在每个时段离场是等可能的。为吸引顾客，每个顾客可以参加一次抽奖活动。

    (1) 用表示甲乙玩都不超过小时的付费情况，求甲、乙二人付费之和为44元的概率；

    (2)抽奖活动的规则是：顾客通过操作按键使电脑自动产生两个[0，1]之间的均匀随机数，并按如右所示的程序框图执行．若电脑显示“中奖”，则该顾客中奖；若电脑显示“谢谢”，则不中奖，求顾客中奖的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题p：关于x的方程xa在（1，+∞）上有实根；命题q：方程1表示的曲线是焦点在x轴上的椭圆．

    （1）若p是真命题，求a的取值范围；

    （2）若p∧q是真命题，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C：x2+y2﹣2x﹣4y+m＝0.

    （1）若圆C与直线l：x+2y﹣4＝0相交于M、N两点，且|MN|，求m的值；

    （2）在（1）成立的条件下，过点P（2，1）引圆的切线，求切线方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设、是双曲线： 的两个焦点，是上一点，若，是△的最小内角，且，则双曲线的渐近线方程是（ ）

    A. B.

    C. D.

    查看答案和解析>>

    同步练习册答案