
【题目】某大学为调查来自南方和北方的同龄大学生的身高差异,从2016级的年龄在18~19岁之间的大学生中随机抽取了来自南方和北方的大学生各10名,测量他们的身高,量出的身高如下(单位:cm):
南方:158,170,166,169,180,175,171,176,162,163.
北方:183,173,169,163,179,171,157,175,184,166.

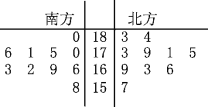
(1)根据抽测结果,画出茎叶图,对来自南方和北方的大学生的身高作比较,写出统计结论.
(2)设抽测的10名南方大学生的平均身高为x cm,将10名南方大学生的身高依次输入如图所示的程序框图进行运算,问输出的s大小为多少?并说明s的统计学意义.
(3)为进一步调查身高与生活习惯的关系,现从来自南方的这10名大学生中随机抽取2名身高不低于170 cm的学生,求身高为176 cm的学生被抽中的概率.
【答案】(1)答案见解析;(2)答案见解析;(3)![]() .
.
【解析】
(1)根据题干中的数据画出茎叶图,根据茎叶图中数据的分散程度和集中程度得到结论;(2)根据框图得到s=42.6,由方差的定义得到s值越小,表示身高越整齐,s值越大,表示身高越参差不齐;(3)从这10名南方大学生中抽出2名身高不低于170 cm的学生有10种情况,事件A含有4个基本事件,故根据古典事件的概率公式得到结果.
.
(1)茎叶图如图所示.统计结论(给出下述四个结论供参考):①北方大学生的平均身高大于南方大学生的平均身高;②南方大学生的身高比北方大学生的身高更整齐;③南方大学生的身高的中位数为169.5 cm,北方大学生的身高的中位数是172 cm;④南方大学生的身高基本上是对称的,而且大多数集中在均值附近,北方大学生的身高分布较为分散.
(2)s=42.6,s表示10位南方大学生身高的方差,是描述身高的离散程度的量.s值越小,表示身高越整齐,s值越大,表示身高越参差不齐.
(3)记“身高为176 cm的学生被抽中”为事件A,从这10名南方大学生中抽出2名身高不低于170 cm的学生有(170,171),(170,175),(170,176),(170,180),(171,175),(171,176),(171,180),(175,176),(175,180),(176,180),共10个基本事件,而事件A含有4个基本事件,故P(A)=![]() =
=![]() .
.


 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:高中数学 来源: 题型:
【题目】A袋中有1个红球和1个黑球,B袋中有2个红球和1个黑球,A袋中任取1个球与B袋中任取1个球互换,这样的互换进行了一次,求:
(1)A袋中红球恰是1个的概率;
(2)A袋中红球至少是1个的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=kx3+3(k﹣1)x2﹣k2+1在x=0,x=4处取得极值.
(1)求常数k的值;
(2)求函数f(x)的单调区间与极值;
(3)设g(x)=f(x)+c,且x∈[﹣1,2],g(x)≥2c+1恒成立,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如下:
成绩/m | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 | 1.85 | 1.90 |
人数 | 2 | 3 | 2 | 3 | 4 | 1 | 1 | 1 |
分别求这些运动员的成绩的众数、中位数、平均数(保留到小数点后两位),并分析这些数据的含义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x2+bln(x+1)在[0,+∞)上单调递减,则b的取值范围( )
A.[0,+∞)
B.[﹣ ![]() ,+∞)
,+∞)
C.(﹣∞,0]
D.(﹣∞,﹣ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)是定义在R上的偶函数,且对任意的x∈R恒有f(x+1)=f(x﹣1),已知当x∈[0,1]时,f(x)=( ![]() )1﹣x , 则
)1﹣x , 则
①2是函数f(x)的一个周期;
②函数f(x)在(1,2)上是减函数,在(2,3)上是增函数;
③函数f(x)的最大值是1,最小值是0;
④x=1是函数f(x)的一个对称轴;
⑤当x∈(3,4)时,f(x)=( ![]() )x﹣3 .
)x﹣3 .
其中所有正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,江的两岸可近似的看成两平行的直线,江岸的一侧有A,B两个蔬菜基地,江的另一侧点C处有一个超市.已知A、B、C中任意两点间的距离为20千米.超市欲在AB之间建一个运输中转站D,A,B两处的蔬菜运抵D处后,再统一经过货轮运抵C处.由于A,B两处蔬菜的差异,这两处的运输费用也不同.如果从A处出发的运输费为每千米2元,从B处出发的运输费为每千米1元,货轮的运输费为每千米3元. 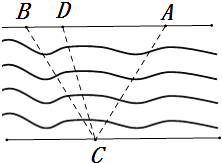
(1)设∠ADC=α,试将运输总费用S(单位:元)表示为α的函数S(α),并写出自变量的取值范围;
(2)问中转站D建在何处时,运输总费用S最小?并求出最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com