
【题目】如图,菱形![]() 的对角线
的对角线![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,
上,![]() ,
,![]() 交
交![]() 于点
于点![]() .将
.将![]() 沿
沿![]() 折到
折到![]() 的位置,
的位置,![]() .
.
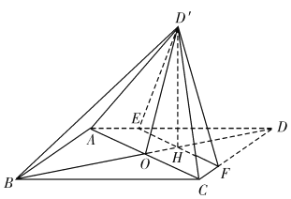
(I)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
科目:高中数学 来源: 题型:
【题目】基于移动网络技术的共享单车被称为“新四大发明”之一,短时间内就风靡全国,给人们带来新的出行体验,某共享单车运营公司的市场研究人员为了了解公司的经营状况,对公司最近6个月的市场占有率![]() 进行了统计,结果如下表:
进行了统计,结果如下表:
月份 | 2018.11 | 2018.12 | 2019.01 | 2019.02 | 2019.03 | 2019.04 |
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
| 11 | 13 | 16 | 15 | 20 | 21 |
(1)请用相关系数说明能否用线性回归模型拟合![]() 与月份代码
与月份代码![]() 之间的关系.如果能,请计算出
之间的关系.如果能,请计算出![]() 关于
关于![]() 的线性回归方程,如果不能,请说明理由;
的线性回归方程,如果不能,请说明理由;
(2)根据调研数据,公司决定再采购一批单车扩大市场,从成本1000元/辆的![]() 型车和800元/辆的
型车和800元/辆的![]() 型车中选购一种,两款单车使用寿命频数如下表:
型车中选购一种,两款单车使用寿命频数如下表:
车型 | 1年 | 2年 | 3年 | 4年 | 总计 |
| 10 | 30 | 40 | 20 | 100 |
| 15 | 40 | 35 | 10 | 100 |
经测算,平均每辆单车每年能为公司带来500元的收入,不考虑除采购成本以外的其它成本,假设每辆单车的使用寿命都是整数年,用频率估计每辆车使用寿命的概率,以平均每辆单车所产生的利润的估计值为决策依据,如果你是公司负责人,会选择哪款车型?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数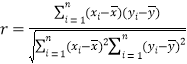 ,
,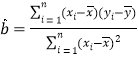 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (α为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系.直线1的极坐标方程为
(α为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系.直线1的极坐标方程为![]() .
.
(Ⅰ)求C的普通方程和l的直角坐标方程;
(Ⅱ)设直线l与x轴和y轴的交点分别为A,B,点M在曲线C上,求△MAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年11月5日至10日,首届中国国际进口博览会在国家会展中心(上海)举行,吸引过来58个“一带一路”沿线国家的超过1000多家企业参展,成为共建“一带一路”的又一个重要支撑。某企业为了参加这次盛会,提升行业竞争力,加大了科技投入;该企业连续6年来得科技投入![]() (百万元)与收益
(百万元)与收益![]() (百万元)的数据统计如下:
(百万元)的数据统计如下:

根据散点图的特点,甲认为样本点分布在指数曲线![]() 的周围,据此他对数据进行了一些初步处理,如下表:
的周围,据此他对数据进行了一些初步处理,如下表:

其中![]() ,
,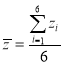 .
.
(1)(![]() )请根据表中数据,建立
)请根据表中数据,建立![]() 关于
关于![]() 的回归方程(保留一位小数);
的回归方程(保留一位小数);
(![]() )根据所建立回归方程,若该企业想在下一年的收益达到2亿,则科技投入的费用至少要多少(其中
)根据所建立回归方程,若该企业想在下一年的收益达到2亿,则科技投入的费用至少要多少(其中![]() )?
)?
(2)乙认为样本点分布在二次曲线![]() 的周围,并计算得回归方程为
的周围,并计算得回归方程为![]() ,以及该回归模型的相关指数
,以及该回归模型的相关指数![]() ,试比较甲乙两位员工所建立的模型,谁的拟合效果更好.
,试比较甲乙两位员工所建立的模型,谁的拟合效果更好.
附:对于一组数据![]() ,
,![]() ,……
,……![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为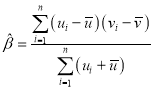 ,
,![]() ,相关指数:
,相关指数: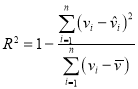 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=f(x),x∈[1,+∞),数列{an}满足![]() ,
,
①函数f(x)是增函数;
②数列{an}是递增数列.
写出一个满足①的函数f(x)的解析式______.
写出一个满足②但不满足①的函数f(x)的解析式______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种物质在时刻![]() 的浓度
的浓度![]() 与
与![]() 的函数关系为
的函数关系为![]() (
(![]() 为常数).在
为常数).在![]() 和
和![]() 测得该物质的浓度分别为
测得该物质的浓度分别为![]() 和
和![]() ,那么在
,那么在![]() 时,该物质的浓度为___________
时,该物质的浓度为___________![]() ;若该物质的浓度小于
;若该物质的浓度小于![]() ,则最小的整数
,则最小的整数![]() 的值为___________.
的值为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com