
【题目】给定数列![]() . 对
. 对![]() ,该数列前
,该数列前![]() 项的最大值记为
项的最大值记为![]() ,后
,后![]() 项
项![]() 的最小值记为
的最小值记为![]() ,
,![]() .
.
(1)设数列![]() 为3,4,7,1. 写出
为3,4,7,1. 写出![]() 的值;
的值;
(2)设![]() 是公比大于
是公比大于![]() 的等比数列,且
的等比数列,且![]() ,证明
,证明![]() 是等比数列;
是等比数列;
(3)若![]() ,证明
,证明![]() 是常数列.
是常数列.
科目:高中数学 来源: 题型:
【题目】已知直线l:y=kx+m与椭圆![]() +
+![]() =1(a>b>0)恰有一个公共点P,l与圆x2+y2=a2相交于A,B两点.
=1(a>b>0)恰有一个公共点P,l与圆x2+y2=a2相交于A,B两点.
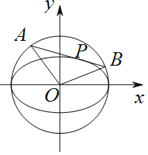
(Ⅰ)求m(用a,b,k表示);
(Ⅱ)当k=-![]() 时,△AOB的面积的最大值为
时,△AOB的面积的最大值为![]() a2,求椭圆的离心率.
a2,求椭圆的离心率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的普及给人们的出行带来了诸多方便,但汽车超速行驶也造成了诸多隐患.为了解汽车通过某一段公路时的车辆行驶情况,现随机抽测了通过这段公路的200辆汽车的行驶速度(单位:km/h),所得数据均在区间![]() 内,其频率分布直方图如图所示.
内,其频率分布直方图如图所示.
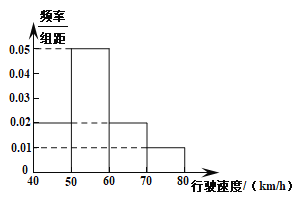
(1)求被抽测的200辆汽车的平均行驶速度.
(2)已知该路段属于事故高发路段,交警部门对此路段过往车辆限速60 km/h,并且对于超速行驶车辆有相应处罚:记分(扣除驾驶员驾照的分数)和罚款.
罚款情况如下:
超速情况 | 10%以内 | 10%~20% | 20%~50% | 50%以上 |
罚款情况 | 0元 | 100元 | 150元 | 500元 |
求被抽测的200辆汽车中超速10%~20%的车辆数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次高三年级统一考试中,数学试卷有一道满分为10分的选做题,学生可以从A,B两道题目中任选一题作答,某校有900名高三学生参加了本次考试,为了了解该校学生解答该选做题的得分情况,计划从900名学生的选做题成绩中随机抽取一个容量为10的样本,为此将900名学生的选做题成绩随机编号为001,002,…,900.若采用分层随机抽样,按照学生选择A题目或B题目,将成绩分为两层,且样本中选择A题目的成绩有8个,平均数为7,方差为4;样本中选择B题目的成绩有2个,平均数为8,方差为1.试用样本估计该校900名学生的选做题得分的平均数与方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知数列![]() 中,
中,![]() ,前项和
,前项和![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列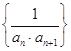 的前项和为
的前项和为![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 对一切正整数都成立?若存在,求出
对一切正整数都成立?若存在,求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,
,![]() (n∈N*).
(n∈N*).
(1)证明数列![]() 是等比数列,求出数列
是等比数列,求出数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() ;
;
(3)数列![]() 中是否存在三项,它们可以构成等差数列?若存在,求出一组符合条件的项;若不存在,说明理由.
中是否存在三项,它们可以构成等差数列?若存在,求出一组符合条件的项;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com