
【题目】如图,已知椭圆C:![]() 的左、右项点分别为A1,A2,左右焦点分别为F1,F2,离心率为
的左、右项点分别为A1,A2,左右焦点分别为F1,F2,离心率为![]() ,|F1F2|=
,|F1F2|=![]() ,O为坐标原点.
,O为坐标原点.
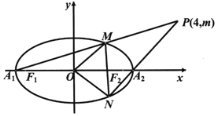
(1)求椭圆C的方程;
(2)设过点P(4,m)的直线PA1,PA2与椭圆分别交于点M,N,其中m>0,求![]() 的面积S的最大值.
的面积S的最大值.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)由离心率为![]() ,|F1F2|=2
,|F1F2|=2![]() ,列式计算a,b,即可得椭圆C的方程.
,列式计算a,b,即可得椭圆C的方程.
(2)将直线PA1,PA1的方程:y![]() ,y
,y![]() 分别与椭圆方程联立,得到M、N的坐标,可得直线MN过定点(1,0),故设MN的方程为:x=ty+1,由
分别与椭圆方程联立,得到M、N的坐标,可得直线MN过定点(1,0),故设MN的方程为:x=ty+1,由![]() 结合韦达定理,可得△OMN的面积S
结合韦达定理,可得△OMN的面积S![]() 2
2![]() ,再利用函数单调性即可求出面积最大值.
,再利用函数单调性即可求出面积最大值.
(1)∵离心率为![]() ,
,![]() ,
,
∴ ,∴
,∴![]() ,
,![]() ,则b=1
,则b=1
∴椭圆C的方程的方程为:![]()
(2)由(1)得A1(-2,0),A2(2,0),
直线PA1,PA1的方程分别为:![]() ,
,![]()
由 ,得
,得![]()
∴![]() ,可得
,可得![]() ,
,![]()
由 ,可得
,可得![]()
∴![]() ,可得
,可得![]() ,
,![]()
![]() ,
,
直线MN的方程为:![]() ,
,
![]()
![]()
![]()
可得直线MN过定点(1,0),故设MN的方程为:![]()
由 得
得![]()
设![]() ,
,![]() ,则
,则![]() ,
,![]()
∴![]() ,
,
∴![]() 的面积
的面积![]()
令![]() ,则
,则![]()
∵![]() ,且函数
,且函数![]() 在
在![]() 递增,
递增,
∴当![]() ,S取得最大值
,S取得最大值![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数y= 4cos2x+4![]() sinxcosx-2,(x∈R)
sinxcosx-2,(x∈R)
(1)求函数的最小正周期;
(2)求函数的最大值及其相对应的x值;
(3)写出函数的单调增区间;
(4)写出函数的对称轴
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,AB=AC=1,BB1=2,∠ABB1=60°.
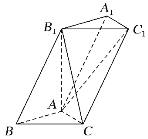
(I) 证明:AB⊥平面AB1C;
(II) 若B1C=2,求AC1与平面BCB1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,新冠肺炎疫情袭击全国,对人民生命安全和生产生活造成严重影响.在党和政府强有力的抗疫领导下,我国控制住疫情后,一方面防止境外疫情输入,另一方面逐步复工复产,减轻经济下降对企业和民众带来的损失.为降低疫情影响,某厂家拟在2020年举行某产品的促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() 万件与年促销费用
万件与年促销费用![]() 万元(
万元(![]() )满足
)满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销售量只能是2万件.已知生产该产品的固定投入为8万元,每生产一万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(此处每件产品年平均成本按
为常数),如果不搞促销活动,则该产品的年销售量只能是2万件.已知生产该产品的固定投入为8万元,每生产一万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(此处每件产品年平均成本按![]() 元来计算)
元来计算)
(1)将2020年该产品的利润![]() 万元表示为年促销费用
万元表示为年促销费用![]() 万元的函数;
万元的函数;
(2)该厂家2020年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国第一高摩天轮“南昌之星摩天轮”高度为![]() ,其中心
,其中心![]() 距地面
距地面![]() ,半径为
,半径为![]() ,若某人从最低点
,若某人从最低点![]() 处登上摩天轮,摩天轮匀速旋转,那么此人与地面的距离将随时间
处登上摩天轮,摩天轮匀速旋转,那么此人与地面的距离将随时间![]() 变化,
变化,![]() 后达到最高点,从登上摩天轮时开始计时.
后达到最高点,从登上摩天轮时开始计时.
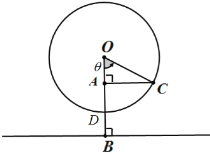
(1)求出人与地面距离![]() 与时间
与时间![]() 的函数解析式;
的函数解析式;
(2)从登上摩天轮到旋转一周过程中,有多长时间人与地面距离大于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知具有线性相关关系的两个变量![]() 之间的几组数据如下表所示:
之间的几组数据如下表所示:
| 2 | 4 | 6 | 8 | 10 |
| 3 | 6 | 7 | 10 | 12 |
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计当
,并估计当![]() 时,
时, ![]() 的值;
的值;
(2)将表格中的数据看作五个点的坐标,则从这五个点中随机抽取2个点,求恰有1个点落在直线![]() 右下方的概率.
右下方的概率.
参考公式: 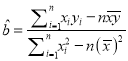 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 是椭圆
是椭圆![]() 的左顶点,经过左焦点
的左顶点,经过左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,求
两点,求![]() 与
与![]() 的面积之差的绝对值的最大值.(
的面积之差的绝对值的最大值.(![]() 为坐标原点)
为坐标原点)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知圆心在![]() 轴上的圆
轴上的圆![]() 经过两点
经过两点![]() 和
和![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)当![]() 时,
时,![]() 为直线
为直线![]() 上的定点,若圆
上的定点,若圆![]() 上存在唯一一点
上存在唯一一点![]() 满足
满足![]() ,求定点
,求定点![]() 的坐标;
的坐标;
(3)设点A,B为圆![]() 上任意两个不同的点,若以AB为直径的圆与直线
上任意两个不同的点,若以AB为直径的圆与直线![]() 都没有公共点,求实数
都没有公共点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com