
【题目】已知![]() ,在区间
,在区间![]() 上存在三个不同的实数
上存在三个不同的实数![]() ,使得以
,使得以![]() 为边长的三角形是直角三角形,则
为边长的三角形是直角三角形,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,
, ![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 把![]() 上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
B. 把![]() 上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
C. 把曲线![]() 向右平移
向右平移![]() 个单位长度,再把得到的曲线上各点横坐标缩短到原来的
个单位长度,再把得到的曲线上各点横坐标缩短到原来的![]() ,纵坐标不变,得到曲线
,纵坐标不变,得到曲线![]()
D. 把曲线![]() 向右平移
向右平移![]() 个单位长度,再把得到的曲线上各点横坐标缩短到原来的
个单位长度,再把得到的曲线上各点横坐标缩短到原来的![]() ,纵坐标不变,得到曲线
,纵坐标不变,得到曲线![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为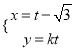 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为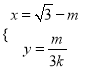 (
(![]() 为参数),设
为参数),设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时,
变化时, ![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)写出![]() 的普遍方程及参数方程;
的普遍方程及参数方程;
(2)以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,设曲线
轴正半轴为极轴建立极坐标系,设曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到
到![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别是
的左右焦点分别是![]() ,椭圆C的上顶点到直线
,椭圆C的上顶点到直线![]() 的距离为
的距离为![]() ,过
,过![]() 且垂直于x轴的直线与椭圆C相交于M,N两点,
且垂直于x轴的直线与椭圆C相交于M,N两点,
且|MN|=1。
(I)求椭圆![]() 的方程;
的方程;
(II)过点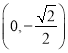 的直线与椭圆C相交于P,Q两点,点
的直线与椭圆C相交于P,Q两点,点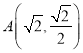 ),且
),且![]() ,求直线
,求直线![]() 的方程。
的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问某地100名高中学生在选择座位时是否挑同桌,得到如下![]() 列联表:
列联表:
男生 | 女生 | 合计 | |
挑同桌 | 30 | 40 | 70 |
不挑同桌 | 20 | 10 | 30 |
总计 | 50 | 50 | 100 |
![]() Ⅰ
Ⅰ![]() 从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本,现从这5人中随机选取3人做深度采访,求这3名学生中至少有2名要挑同桌的概率;
从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本,现从这5人中随机选取3人做深度采访,求这3名学生中至少有2名要挑同桌的概率;
![]() Ⅱ
Ⅱ![]() 根据以上
根据以上![]() 列联表,是否有
列联表,是否有![]() 以上的把握认为“性别与在选择座位时是否挑同桌”有关?
以上的把握认为“性别与在选择座位时是否挑同桌”有关?
下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() 参考公式:
参考公式: ![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是定义在
是定义在![]() 上且满足如下条件的函数
上且满足如下条件的函数![]() 组成的集合:①对任意的
组成的集合:①对任意的![]() ,都有
,都有![]() ②存在常数
②存在常数![]() 使得对任意的
使得对任意的![]() ,都有
,都有![]() .
.
(1)设![]() 问
问![]() 是否属于
是否属于![]() ?说明理由;
?说明理由;
(2)若![]() 如果存在
如果存在![]() 使得
使得![]() 证明:这样的
证明:这样的![]() 是唯一的;
是唯一的;
(3)设![]() 且
且![]() 试求
试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x2+alnx.
x2+alnx.
(1)若a=﹣1,求函数f(x)的极值,并指出极大值还是极小值;
(2)若a=1,求函数f(x)在[1,e]上的最值;
(3)若a=1,求证:在区间[1,+∞)上,函数f(x)的图象在g(x)=![]() x3的图象下方.
x3的图象下方.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
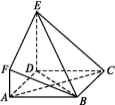
(1)求二面角F-BE-D的余弦值;
(2)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com