
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:(1)由![]() ,可得
,可得![]() ,两式相减可化为
,两式相减可化为![]() ,可得数列
,可得数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,从而可得结果;(2)由(1)可得
的等比数列,从而可得结果;(2)由(1)可得![]() .利用错位相减法,结合等比数列的求和公式可得数列
.利用错位相减法,结合等比数列的求和公式可得数列![]() 的前
的前![]() 项和
项和![]() .
.
详解:(1)∵2Sn+3=3an, ①
∴2Sn-1+3=3an-1, (n≥2) ②
①-②得2Sn-2Sn-1=3an-3an-1=2an,
则![]() =3 (n≥2),
=3 (n≥2),
在①式中,令n=1,得a1=3.
∴数列{an}是首项为3,公比为3的等比数列,
∴an=3n.
(2)bn=an·log3an+2=3n·log33n+2=(n+2)·3n.
所以Tn=3·31+4·32+5·33+…+(n+1)·3n-1+(n+2)·3n, ①
则 3Tn= 3·32+4·33+…+n·3n-1+(n+1)·3n+(n+2)·3n+1, ②
①-②得,
-2Tn=9+1 (32+33+…+3n-1+3n)-(n+2)·3n+1,
=9+![]() -(n+2)·3n+1
-(n+2)·3n+1
=![]() -
-![]() ×3n+1.
×3n+1.
所以Tn=![]() ×3n+1-
×3n+1-![]() .
.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
【题目】十八届五中全会公报指出:努力促进人口均衡发展,坚持计划生育的基本国策,完善人口发展战略,全面实施一对夫妇可生育两个孩子的政策。提高生殖健康、妇幼保健、托幼等公共服务水平。为了解适龄公务员对放开生育二胎政策的态度,某部门随机调查了200位30到40岁的公务员,得到情况如下表:

(Ⅰ)是否有99%以上的把握认为“生二胎与性别有关”,并说明理由;
(Ⅱ)将频率看作概率,现从社会上随机抽取甲、乙、丙3位30到40 岁的男公务员,求这三人中至少有一人要生二胎的概率.
附:![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线的焦点在x轴上,焦距为![]() ,实轴长为2
,实轴长为2
(1)求双曲线的标准方程与渐近线方程。
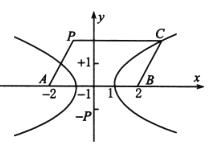
(2)若点 ![]() 在该双曲线上运动,且
在该双曲线上运动,且![]() ,
,![]() ,求以
,求以 ![]() ,
,![]() 为相邻两边的平行四边形
为相邻两边的平行四边形 ![]() 的顶点
的顶点 ![]() 的轨迹.
的轨迹.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将五个1,五个2,五个3,五个4,五个5共25个数填入一个5行5列的表格内(每格填入一个数),使得同一行中任何两数之差的绝对值不超过2,考查每行中五个数之和,记这五个和的最小值为![]() ,则
,则![]() 的最大值为( )
的最大值为( )
A. ![]() B. 9 C. 10 D. 11
B. 9 C. 10 D. 11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中装有![]() 个形状大小完全相同的小球,球的编号分别为
个形状大小完全相同的小球,球的编号分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)若从袋中每次随机抽取![]() 个球,有放回的抽取
个球,有放回的抽取![]() 次,求取出的两个球编号之和为
次,求取出的两个球编号之和为![]() 的概率.
的概率.
(Ⅱ)若从袋中每次随机抽取![]() 个球,有放回的抽取
个球,有放回的抽取![]() 次,求恰有
次,求恰有![]() 次抽到
次抽到![]() 号球的概率.
号球的概率.
(Ⅲ)若一次从袋中随机抽取![]() 个球,记球的最大编号为
个球,记球的最大编号为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
(Ⅳ)若从袋中每次随机抽取![]() 个球,有放回的抽取
个球,有放回的抽取![]() 次,记球的最大编号为
次,记球的最大编号为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
:![]() 与
与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 坐标为
坐标为![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,交直线
的垂线,交直线![]() 于点
于点![]() .记过
.记过![]() 、
、![]() 、
、![]() 三点的圆为圆
三点的圆为圆![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)求过点![]() 与圆
与圆![]() 相交所得弦长为8的直线方程.
相交所得弦长为8的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县城出租车的收费标准是:起步价是![]() 元(乘车不超过
元(乘车不超过![]() 千米);行驶
千米);行驶![]() 千米后,每千米车费1.2元;行驶
千米后,每千米车费1.2元;行驶![]() 千米后,每千米车费1.8元.
千米后,每千米车费1.8元.
(1)写出车费与路程的关系式;
(2)一顾客计划行程![]() 千米,为了省钱,他设计了三种乘车方案:
千米,为了省钱,他设计了三种乘车方案:
①不换车:乘一辆出租车行![]() 千米;
千米;
②分两段乘车:先乘一辆车行![]() 千米,换乘另一辆车再行
千米,换乘另一辆车再行![]() 千米;
千米;
③分三段乘车:每乘![]() 千米换一次车.
千米换一次车.
问哪一种方案最省钱.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com