

| A. | $\frac{5}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{4}{3}$ |
分析 首先根据三视图,把平面图形转化成立体图形进一步根据几何体的体积公式求出结果
解答 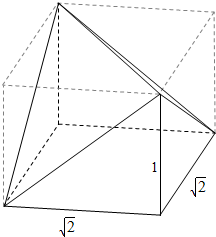 解:根据三视图得知:该几何体是长、宽、高为$\sqrt{2}$、$\sqrt{2}$、1的长方体去掉一个外边的左上角的三棱锥和去掉一个里边右上角的三棱锥的多面体,如图
解:根据三视图得知:该几何体是长、宽、高为$\sqrt{2}$、$\sqrt{2}$、1的长方体去掉一个外边的左上角的三棱锥和去掉一个里边右上角的三棱锥的多面体,如图
所以:该几何体的体积为:V=V长方体-2V三棱锥
=$\sqrt{2}$×$\sqrt{2}$×1-2×$\frac{1}{3}$×$\frac{1}{2}$×$\sqrt{2}×\sqrt{2}$=2-$\frac{2}{3}$=$\frac{4}{3}$.
故选:D.
点评 本题考查的知识要点:三视图和立体图的关系,几何体的体积公式的应用,主要考查学生的空间想象能力和对知识的应用能力.


科目:高中数学 来源: 题型:选择题
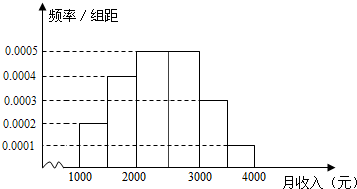 某市统计局就某地居民的月收入调查了10 000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1 000,1 500)内).根据频率分布直方图算出样本数据的中位数是( )
某市统计局就某地居民的月收入调查了10 000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1 000,1 500)内).根据频率分布直方图算出样本数据的中位数是( )| A. | 2360 | B. | 2380 | C. | 2400 | D. | 2420 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com