
【题目】已知函数f(x)=x2+b图象上的点P(2,1)关于直线y=x的对称点Q在函数g(x)=lnx+a上.
(Ⅰ)求函数h(x)=g(x)-f(x)的最大值;
(Ⅱ)对任意x1∈[1,e],x2∈![]() ,是否存在实数k,使得不等式
,是否存在实数k,使得不等式![]() 成立,若存在,请求出实数k的取值范围;若不存在,请说明理由.
成立,若存在,请求出实数k的取值范围;若不存在,请说明理由.
【答案】(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ) 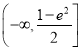 .
.
【解析】试题分析:(Ⅰ)由题意得方程组![]() ,解得a,b的值,设h(x)=g(x)﹣f(x)=lnx﹣x2+5,通过求导得出h(x)在(
,解得a,b的值,设h(x)=g(x)﹣f(x)=lnx﹣x2+5,通过求导得出h(x)在(![]() ,+∞)递减,在(0,
,+∞)递减,在(0, ![]() )递增;从而求出函数h(x)的最大值.
)递增;从而求出函数h(x)的最大值.
(Ⅱ)设G(x)=2k[g(x)﹣2]+f(x)+3=2klnx+x2,通过讨论①k≥0,②0<![]() ,③1<
,③1<![]() ≤e,④
≤e,④![]() >e的情况,从而求出k的范围.
>e的情况,从而求出k的范围.
试题解析:
(Ⅰ)点P(2,1)关于直线y=x的对称点Q(1,2),
∴![]() ,解得
,解得![]() ,
,
设h(x)=g(x)-f(x)=lnx-x2+5,
h′(x)=![]() -2x
-2x
=-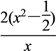 =-
=-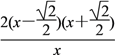 ,
,
∵x∈(0,+∞),
∴当x∈(![]() ,+∞)时,h′(x)<0;当x∈(0,
,+∞)时,h′(x)<0;当x∈(0,![]() )时,h′(x)>0,
)时,h′(x)>0,
∴h(x)在(![]() ,+∞)上单调递减;在(0,
,+∞)上单调递减;在(0,![]() )上单调递增,
)上单调递增,
∴h(x)max=h(![]() )=
)=![]() -
-![]() ln2,
ln2,
(Ⅱ)设T(x)=ln![]() =2lnx,
=2lnx,
∵ T′(x)=![]() ,当x∈[
,当x∈[![]() ,e2]时,T′(x)>0,即单调递增,
,e2]时,T′(x)>0,即单调递增,
∴在[![]() ,e2]上T(x)min=T(
,e2]上T(x)min=T(![]() )=lne=1,
)=lne=1,
设G(x)=2k![]() +f(x)+3=2klnx+x2,
+f(x)+3=2klnx+x2,
G′(x)=![]() +2x=
+2x=![]() ,
,
①当k≥0时,在[1,e]上G′(x)>0,即单调递增,即G(x)max=G(e)=2k+e2,
依题得2k+e2≤1,∴k≤![]() ,
,
又∵k≥0,∴k无解;
②当0<![]() ≤1,即-1≤k<0时,
≤1,即-1≤k<0时,
在[1,e]上G′(x)>0,即单调递增,
G(x)max=G(e)=2k+e2 ,
依题得2k+e2≤1,∴k≤![]() ,
,
又∵-1≤k<0,∴k无解;
③当1<![]() ≤e,即-e2≤k<-1时,
≤e,即-e2≤k<-1时,
在[1,![]() ]上G′(x)<0,即单调递减;
]上G′(x)<0,即单调递减;
在[![]() ,e]上 G′(x)>0,即单调递增,
,e]上 G′(x)>0,即单调递增,
又∵G(e)=2k+e2,G(1)=1,
当G(e)≤G(1),即k≤![]() 时,G(x)max=G(1)=1,显然1≤1成立;
时,G(x)max=G(1)=1,显然1≤1成立;
∵-e2<![]() <-1,∴-e2≤k≤
<-1,∴-e2≤k≤![]() ;
;
当G(e)>G(1),即k>![]() 时,G(x)max=G(e)=2k+e2,
时,G(x)max=G(e)=2k+e2,
由2k+e2≤1得k≤![]() ,∴k无解;
,∴k无解;
④当![]() >e,即k<-e2时,在[1,e]上G′(x)<0,即单调递减,G(x)max=G(1)=1,显然1≤1成立,
>e,即k<-e2时,在[1,e]上G′(x)<0,即单调递减,G(x)max=G(1)=1,显然1≤1成立,
综上,实数k的取值范围为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分)己知函数f(x)= ![]()
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求证:当x∈(0,1)时,f(x)>2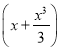
(3)设实数k使得f(x)>k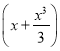 对x∈(0,1)恒成立,求k的最大值.
对x∈(0,1)恒成立,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1 ,在△ABC中,AB=BC=2, ∠B=90°,D为BC边上一点,以边AC为对角线做平行四边形ADCE,沿AC将△ACE折起,使得平面ACE ⊥平面ABC,如图2.
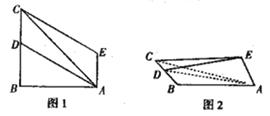
(1)在图 2中,设M为AC的中点,求证:BM丄AE;
(2)在图2中,当DE最小时,求二面角A -DE-C的平面角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】园林管理处拟在公园某区域规划建设一半径为![]() 米圆心角为
米圆心角为![]() (弧度)的扇形景观水池,其中
(弧度)的扇形景观水池,其中![]() 为扇形
为扇形![]() 的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过
的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过![]() 万元,水池造价为每平方米
万元,水池造价为每平方米![]() 元,步道造价为每米
元,步道造价为每米![]() 元.
元.
(1)当![]() 和
和![]() 分别为多少时,可使广场面积最大,并求出最大值;
分别为多少时,可使广场面积最大,并求出最大值;
(2)若要求步道长为![]() 米,则可设计出水池最大面积是多少.
米,则可设计出水池最大面积是多少.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(-2,0),B(2,0),曲线C上的动点P满足![]() .
.
(1)求曲线C的方程;
(2)若过定点M(0,-2)的直线l与曲线C有公共点,求直线l的斜率k的取值范围;
(3)若动点Q(x,y)在曲线C上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,放置的边长为1的正方形PABC沿x轴滚动,点B恰好经过原点.设顶点P(x,y)的轨迹方程是y=f(x),则对函数y=f(x)有下列判断:
①若-2≤x≤2,则函数y=f(x)是偶函数;
②对任意的x∈R,都有f(x+2)=f(x-2);
③函数y=f(x)在区间[2,3]上单调递减;
④函数y=f(x)在区间[4,6]上是减函数.
其中判断正确的序号是________.(写出所有正确结论的序号)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,A、B、C的对边分别为a,b,c,已知向量![]() ,n=(c,b-2a),且m·n=0.
,n=(c,b-2a),且m·n=0.
(1)求角C的大小;
(2)若点D为边AB上一点,且满足![]() ,
, ![]() ,
, ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·合肥市质检)已知点F为椭圆E: ![]() (a>b>0)的左焦点,且两焦点与短轴的一个顶点构成一个等边三角形,直线
(a>b>0)的左焦点,且两焦点与短轴的一个顶点构成一个等边三角形,直线![]() 与椭圆E有且仅有一个交点M.
与椭圆E有且仅有一个交点M.
(1)求椭圆E的方程;
(2)设直线![]() 与y轴交于P,过点P的直线l与椭圆E交于不同的两点A,B,若λ|PM|2=|PA|·|PB|,求实数λ的取值范围.
与y轴交于P,过点P的直线l与椭圆E交于不同的两点A,B,若λ|PM|2=|PA|·|PB|,求实数λ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com