
【题目】已知函数f(x)=|x﹣2|.
(1)解不等式f(x)+f(x+1)≥5;
(2)若|a|>1且 ![]() ,证明:|b|>2.
,证明:|b|>2.
【答案】
(1)解:原不等式等价于|x﹣2|+|x﹣1|≥5,
当x>2时,不等式可化为:(x﹣2)+(x﹣1)≥5,
解得:x≥4,
当1≤x≤2时,不等式可化为(2﹣x)+(x﹣1)≥5,1≥5,无解,
x<1时,不等式可化为:(2﹣x)+(1﹣x)≥5,解得:x≤﹣1,
综上,不等式的解集是{x|x≥4或x≤﹣1}
(2)证明: ![]()
|ab﹣2|>|a|| ![]() ﹣2|
﹣2|
|ab﹣2|>|b﹣2a|
(ab﹣2)2>(b﹣2a)2
a2b2+4﹣b2﹣4a2>0
(a2﹣1)(b2﹣4)>0,
∵|a|>1,
∴a2﹣1>0,
∴b2﹣4>0,
∴|b|>2,证毕
【解析】(1)通过讨论x的范围,去掉绝对值号,解不等式即可;(2)求出f(ab)和f( ![]() ),代入不等式,问题转化为|ab﹣2|>|b﹣2a|,平方证明即可.
),代入不等式,问题转化为|ab﹣2|>|b﹣2a|,平方证明即可.
【考点精析】认真审题,首先需要了解绝对值不等式的解法(含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号).


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() 抛物线
抛物线![]() 上存在一点
上存在一点![]() 到焦点
到焦点![]() 的距离等于3.
的距离等于3.
(1)求抛物线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点(
两点(![]() 两点在
两点在![]() 轴上方),点
轴上方),点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,且
,且![]() ,求
,求![]() 的外接圆的方程.
的外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|﹣2|x|.
(1)求不等式f(x)≤﹣6的解集;
(2)若存在实数x满足f(x)=log2a,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高二某班共有20名男生,在一次体验中这20名男生被平均分成两个小组,第一组和第二组男生的身高(单位: ![]() )的茎叶图如下:
)的茎叶图如下:

(1)根据茎叶图,分别写出两组学生身高的中位数;
(2)从该班身高超过![]() 的7名男生中随机选出2名男生参加校篮球队集训,求这2名男生至少有1人来自第二组的概率;
的7名男生中随机选出2名男生参加校篮球队集训,求这2名男生至少有1人来自第二组的概率;
(3)在两组身高位于![]() (单位:
(单位: ![]() )的男生中各随机选出2人,设这4人中身高位于
)的男生中各随机选出2人,设这4人中身高位于![]() (单位:
(单位: ![]() )的人数为
)的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有价值10万元的一条流水线,要提高该流水线的生产能力,就要对其进行技术改造,改造就需要投入,相应就要提高产品附加值,假设附加值![]() 万元与技术改造投入
万元与技术改造投入![]() 万元之间的关系满足:①
万元之间的关系满足:① ![]() 与
与![]() 和
和![]() 的乘积成正比;② 当
的乘积成正比;② 当![]() 时,
时,![]() ;③
;③![]() ,其中
,其中![]() 为常数,且
为常数,且![]() .
.
(1)设![]() ,求出
,求出![]() 的表达式,并求出
的表达式,并求出![]() 的定义域;
的定义域;
(2)求出附加值![]() 的最大值,并求出此时的技术改造投入的
的最大值,并求出此时的技术改造投入的![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司试销一种成本单价为500元的新产品,规定试销时销售单价不低于成本单价,又不高于800元.经试销调查,发现销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=kx+b(k≠0),函数图象如图所示.

(1)根据图象,求一次函数y=kx+b(k≠0)的表达式;
(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元.试问销售单价定为多少时,该公司可获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有工人1000名,为了提高工人的生产技能,特组织工人参加培训.其中250名工人参加过短期培训(称为![]() 类工人),另外750名工人参加过长期培训(称为
类工人),另外750名工人参加过长期培训(称为![]() 类工人).现从该工厂的工人中共抽查了100名工人作为样本,调查他们的生产能力(生产能力是指工人一天加工的零件数),得到
类工人).现从该工厂的工人中共抽查了100名工人作为样本,调查他们的生产能力(生产能力是指工人一天加工的零件数),得到![]() 类工人生产能力的茎叶图(图1),
类工人生产能力的茎叶图(图1),![]() 类工人生产能力的频率分布直方图(图2).
类工人生产能力的频率分布直方图(图2).
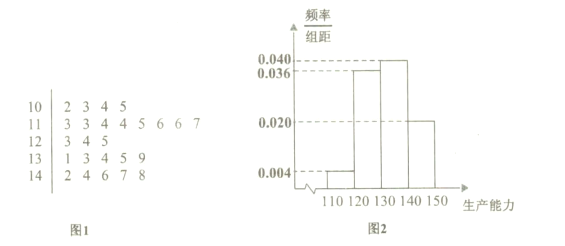
(1)在样本中求![]() 类工人生产能力的中位数,并估计
类工人生产能力的中位数,并估计![]() 类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
(2)若规定生产能力在![]() 内为能力优秀,现以样本中频率作为概率,从1000名工人中按分层抽样共抽取
内为能力优秀,现以样本中频率作为概率,从1000名工人中按分层抽样共抽取![]() 名工人进行调查,请估计这
名工人进行调查,请估计这![]() 名工人中的各类人数,完成下面的
名工人中的各类人数,完成下面的![]() 列联表.
列联表.

若研究得到在犯错误的概率不超过![]() 的前提下,认为生产能力与培训时间长短有关,则
的前提下,认为生产能力与培训时间长短有关,则![]() 的最小值为多少?
的最小值为多少?
参考数据:

参考公式: 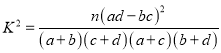 ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com