
| A. | $(\frac{{5-\sqrt{3}}}{4},1)$ | B. | $(1,\frac{{5+\sqrt{3}}}{4})$ | C. | $(\frac{1}{2},1)$ | D. | (1,2) |
分析 根据所给的新定义,写出函数的分段形式的解析式,画出函数的图象,在图象上可以看出当直线与函数的图象有三个不同的交点时m的取值,根据一元二次方程的根与系数之间的关系,写出两个根的积和第三个根,表示出三个根之和,并判断出函数的单调性,求出函数的值域,得到结果.
解答 解:∵2x-1≤x-1时,有x≤0,
∴根据题意得f(x)=$\left\{\begin{array}{l}(2x-1)^{2}-(2x-1)(x-1),x≤0\\(x-1)^{2}-(2x-1)(x-1),x>0\end{array}\right.$,
即f(x)=$\left\{\begin{array}{l}2{x}^{2}-x,x≤0\\{-x}^{2}+x,x>0\end{array}\right.$,
画出函数的图象,如下图所示: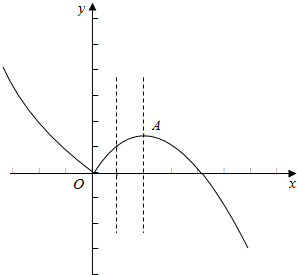
从图象上观察当关于x的方程为f(x)=t(t∈R)恰有三个互不相等的实数根时,t的取值范围是(0,$\frac{1}{4}$),
当-x2+x=t时,有x1+x2=1,
当2x2-x=t时,由于直线与抛物线的交点在y轴的左边,得到x3=$\frac{1-\sqrt{1+8t}}{4}$,
∴x1+x2+x3=1+$\frac{1-\sqrt{1+8t}}{4}$=$\frac{5-\sqrt{1+8t}}{4}$,t∈(0,$\frac{1}{4}$),
令y=$\frac{5-\sqrt{1+8t}}{4}$,t∈(0,$\frac{1}{4}$),则函数是减函数,
又由t=0时,y=1,t=$\frac{1}{4}$时,y=$\frac{5-\sqrt{3}}{4}$,
故x1+x2+x3的取值范围是$(\frac{5-\sqrt{3}}{4},1)$,
故选:A
点评 本题考查分段函数的图象,考查新定义问题,这种问题解决的关键是根据新定义写出符合条件的解析式,本题是一个综合问题,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | tanα | B. | -cosα | C. | sinα | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
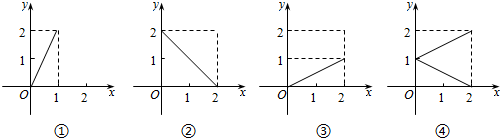
| A. | ①②③④ | B. | ①②③ | C. | ②③ | D. | ② |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com