
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)判断函数![]() 能否有3个零点?若能,求出
能否有3个零点?若能,求出![]() 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.
【答案】(1)见解析;(2)不可能有![]() 个零点;说明见解析
个零点;说明见解析
【解析】
(1)求导后,根据导函数零点的分布情况在![]() 不同的取值范围情况下讨论导函数的正负,从而得到函数的单调性;(2)采用反证法,假设有
不同的取值范围情况下讨论导函数的正负,从而得到函数的单调性;(2)采用反证法,假设有![]() 个零点,可知需满足
个零点,可知需满足![]() 或
或![]() ;当
;当![]() 时,可得极大值
时,可得极大值![]() ,从而知不可能有
,从而知不可能有![]() 个零点;当
个零点;当![]() 时,可得极大值
时,可得极大值![]() ,将其看做关于
,将其看做关于![]() 的函数,通过导数可判断出
的函数,通过导数可判断出![]() ,从而可知不可能有
,从而可知不可能有![]() 个零点;可知假设错误,即
个零点;可知假设错误,即![]() 不可能有
不可能有![]() 个零点.
个零点.
(1)由题意知:函数定义域为![]()
![]()
①若![]() ,则
,则![]()
当![]() 时,
时,![]() ,则
,则![]() 为减函数
为减函数
当![]() 时,
时,![]() ,则
,则![]() 为增函数
为增函数
②若![]()
当![]() 或
或![]() 时,
时,![]() ,则
,则![]() 为增函数
为增函数
当![]() 时,
时,![]() ,则
,则![]() 为减函数
为减函数
③若![]() ,则
,则![]() ,故
,故![]() 在
在![]() 上增函数
上增函数
④若![]()
当![]() 或
或![]() 时,
时,![]() ,则
,则![]() 为增函数
为增函数
当![]() 时,
时,![]() ,则
,则![]() 为减函数
为减函数
(2)若函数![]() 有
有![]() 个零点,由(1)可知,必有
个零点,由(1)可知,必有![]() 或
或![]()
①若![]() ,由(1)可知
,由(1)可知![]() 在
在![]() 处取得极大值,在
处取得极大值,在![]() 处取得极小值
处取得极小值
![]()
![]() 此时
此时![]() 不可能有
不可能有![]() 个零点
个零点
②若![]() ,由(1)可知
,由(1)可知![]() 在
在![]() 处取得极大值,在
处取得极大值,在![]() 处取得极小值
处取得极小值
![]()
则![]() ,
,![]()
![]()
![]() ,即
,即![]()
![]() 在
在![]() 上单调递增
上单调递增
![]()
![]() 在
在![]() 上单调递减
上单调递减
当![]() 时,
时,![]()
![]()
![]() 此时
此时![]() 不可能有
不可能有![]() 个零点
个零点
综上所述:函数![]() 不可能有
不可能有![]() 个零点
个零点


科目:高中数学 来源: 题型:
【题目】有甲、乙两家公司都需要招聘求职者,这两家公司的聘用信息如下:
甲公司 | 乙公司 | ||||||||
职位 | A | B | C | D | 职位 | A | B | C | D |
月薪/千元 | 5 | 6 | 7 | 8 | 月薪/千元 | 4 | 6 | 8 | 10 |
获得相应职位概率 | 0.4 | 0.3 | 0.2 | 0.1 | 获得相应职位概率 | 0.4 | 0.3 | 0.2 | 0.1 |
(1)若两人分别去应聘甲、乙两家公司的C职位,记这两人被甲、乙两家公司的C职位录用的人数和为![]() ,求
,求![]() 的分布列;
的分布列;
(2)根据甲、乙两家公司的聘用信息,如果你是该求职者,你会选择哪一家公司?说明理由。
(3)若小王和小李分别被甲、乙两家公司录用,求小王月薪高于小李的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只药用昆虫的产卵数![]() 与一定范围内与温度
与一定范围内与温度![]() 有关, 现收集了该种药用昆虫的6组观测数据如下表:
有关, 现收集了该种药用昆虫的6组观测数据如下表:
温度 | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数 | 6 | 11 | 20 | 27 | 57 | 77 |
(1)若用线性回归模型,求![]() 关于
关于![]() 的回归方程
的回归方程![]() =
=![]() x+
x+![]() (精确到0.1);
(精确到0.1);
(2)若用非线性回归模型求![]() 关
关![]() 的回归方程为
的回归方程为![]()
![]() 且相关指数
且相关指数![]()
( i )试与 (1)中的线性回归模型相比,用![]() 说明哪种模型的拟合效果更好.
说明哪种模型的拟合效果更好.
( ii )用拟合效果好的模型预测温度为![]() 时该种药用昆虫的产卵数(结果取整数).
时该种药用昆虫的产卵数(结果取整数).
附:一组数据(x1,y1), (x2,y2), ...,(xn,yn), 其回归直线![]() =
=![]() x+
x+![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为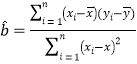 ,
,![]() ,相关指数
,相关指数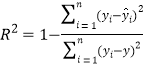 .
.
![]()
![]()
![]()
![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
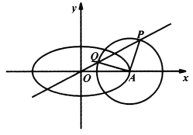
【题目】己知椭圆![]() 的焦距为
的焦距为![]() ,以椭圆C的右顶点A为圆心的圆与直线
,以椭圆C的右顶点A为圆心的圆与直线![]() 相交于P,Q两点,且
相交于P,Q两点,且![]() .
.
(I)求椭圆C的标准方程和圆A的方程。
(II)不过原点的直线l与椭圆C交于M,N两点,已知直线OM,l,ON的斜率![]() 成等比数列,记以线段OM,线段ON为直径的圆的面积分别为
成等比数列,记以线段OM,线段ON为直径的圆的面积分别为![]() 的值是否为定值?若是,求出此值:若不是,说明理由.
的值是否为定值?若是,求出此值:若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“剪刀、石头、布”的游戏规则是:双方齐喊口令,然后同时出拳,握紧的拳头代表“石头”,“食指和中指伸出代表“剪刀”,五指伸开代表“布”。“ 石头”胜“剪刀”, “剪刀”胜“布”, “布”胜“石头”,若所出拳相同则为和局。现甲乙两人通过“剪刀、石头、布”进行比赛。
(1)设甲乙两人每局都随机出“剪刀”、“石头”、“布”中的某一个,求甲胜乙的概率;
(2)最近中国科学家在网上发布了“剪刀、石头、布”的致胜策略,引起了甲的关注,据甲认真观察,乙有以下出拳习惯:①第一局不出“剪刀”; ②连续两局的出拳一定不一样,即如本局出“剪刀”,则下局出“石头”、“布”中的一个。假设甲的分析是正确的,甲据此分析出拳,保证每局都不输给乙,在最多5局的比赛中,谁胜的局数多,谁获胜。游戏结束的条件是:一方胜3局或赛满5局,用![]() 表示游戏结束时的游戏局数,求
表示游戏结束时的游戏局数,求![]() 的分布列和期望。
的分布列和期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家拟举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() 万件与年促销费用
万件与年促销费用![]() 万元(
万元(![]() )满足
)满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将该产品的年利润![]() 万元表示为年促销费用
万元表示为年促销费用![]() 万元的函数;
万元的函数;
(2)该厂家年促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为偶函数,函数
为偶函数,函数![]() 为奇函数。
为奇函数。![]() 对任意实数x恒成立.
对任意实数x恒成立.
(1)求函数![]() 与
与![]() ;
;
(2)设![]() ,
,![]() ,若
,若![]() 对于
对于![]() 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(3)对于(2)中的函数![]() ,若方程
,若方程![]() 没有实数解,实数m的取值范围.
没有实数解,实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com