
【题目】给出下列四种说法:①函数![]() 的单调递增区间是
的单调递增区间是![]() ;②函数
;②函数![]() 与
与![]() 的值域相同;③函数
的值域相同;③函数![]() 与
与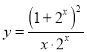 均是奇函数;④若函数
均是奇函数;④若函数![]() 在
在![]() 上有零点,则实数
上有零点,则实数![]() 的取值范围是
的取值范围是![]() .其中正确结论的序号是_______.
.其中正确结论的序号是_______.
科目:高中数学 来源: 题型:
【题目】“吸烟有害健康,吸烟会对身体造成伤害”,哈尔滨市于2012年5月31日规定室内场所禁止吸烟.美国癌症协会研究表明,开始吸烟年龄X分别为16岁、18岁、20岁和22岁者,其得肺癌的相对危险度Y依次为15.10,12.81,9.72,3.21;每天吸烟支数U分别为10,20,30者,其得肺癌的相对危险度V分别为7.5,9.5和16.6,用![]() 表示变量X与Y之间的线性相关系数,用r2表示变量U与V之间的线性相关系数,则下列说法正确的是( )
表示变量X与Y之间的线性相关系数,用r2表示变量U与V之间的线性相关系数,则下列说法正确的是( )
A.r1=r2B.r1>r2>0
C.0<r1<r2D.r1<0<r2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某公司2001年至2017年新产品研发费用![]() (单位:万元)的折线图.为了预测该公司2019年的新产品研发费用,建立了
(单位:万元)的折线图.为了预测该公司2019年的新产品研发费用,建立了![]() 与时间变量
与时间变量![]() 的两个线性回归模型.根据2001年至2017年的数据(时间变量
的两个线性回归模型.根据2001年至2017年的数据(时间变量![]() 的值依次为1,2,…,17)建立模型①:
的值依次为1,2,…,17)建立模型①:![]() ;根据2011年至2017年的数据(时间变量
;根据2011年至2017年的数据(时间变量![]() 的值依次为1,2,…,7)建立模型②:
的值依次为1,2,…,7)建立模型②:![]() .
.

(1)分别利用这两个模型,求该公司2019年的新产品研发费用的预测值;
(2)你认为用哪个模型得到的预测值更可靠?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
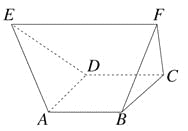
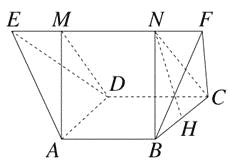
【题目】如图,在多面体ABCDEF中,已知四边形ABCD是边长为1的正方形,且△ADE,△BCF均为正三角形,EF∥AB,EF=2,则该多面体的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市预测2000年到2004年人口总数与年份的关系如下表所示
年份200x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十)万 | 5 | 7 | 8 | 11 | 19 |
(1)请根据上表提供的数据,计算![]() ,用最小二乘法求出
,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]()
(2) 据此估计2005年该城市人口总数。
(参考数值:0×5+1×7+2×8+3×11+4×19=132,![]()
参考公式:用最小二乘法求线性回归方程系数公式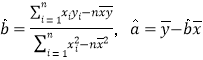 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若函数
,若函数![]() 满足:①在区间
满足:①在区间![]() 上单调递减,②存在常数
上单调递减,②存在常数![]() ,使其值域为
,使其值域为![]() ,则称函数
,则称函数![]() 是函数
是函数![]() 的“渐近函数”.
的“渐近函数”.
(1)判断函数![]() 是不是函数
是不是函数![]() 的“渐近函数”,说明理由;
的“渐近函数”,说明理由;
(2)求证:函数![]() 不是函数
不是函数![]() 的“渐近函数”;
的“渐近函数”;
(3)若函数![]() ,
,![]() ,求证:当且仅当
,求证:当且仅当![]() 时,
时,![]() 是
是![]() 的“渐近函数”.
的“渐近函数”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知数列![]() 中,
中,![]() ,前项和
,前项和![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列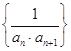 的前项和为
的前项和为![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 对一切正整数都成立?若存在,求出
对一切正整数都成立?若存在,求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 经过点
经过点![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过坐标原点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,过点
两点,过点![]() 作
作![]() 的平行线交椭圆
的平行线交椭圆![]() 于
于![]() 、
、![]() 两点.
两点.
①是否存在常数![]() ,满足
,满足![]() ?若存在,求出这个常数;若不存在,请说明理由;
?若存在,求出这个常数;若不存在,请说明理由;
②若![]() 的面积为
的面积为![]() ,
, ![]() 的面积为
的面积为![]() ,且
,且![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥PABC中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.

(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求直线AN与平面PMN所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com