
分析 (1)利用奇函数的定义,即可求实数m的值;
(2)分类讨论,利用当x∈(p,a-2)时,函数f(x)的值域是(1,+∞),可得结论;
(3)g(x)=-ax2+6x+1x∈[4,5]且a>0,a≠1,分类讨论,求出函数g(x)的最大值.
解答 解:(1)∵函数$f(x)={log_a}\frac{1-mx}{x-1}(a>0,a≠1)$是奇函数.
∴f(-x)+f(x)=0解得m=±1
又 m=1时,表达式无意义,所以m=-1…(2分)
(2)由题设知:函数f(x)的定义域为(1,+∞)∪(-∞,-1),
①当p<a-2≤-1时,有0<a<1.此时f(x)为增函数,
其值域为$(1,+∞)知\left\{\begin{array}{l}log\frac{1+n}{n-1}=1\\ a-2=-1\end{array}\right.$(与题设矛盾,无解);…(5分)
②当1≤p≤a-2时,有a>3.此时f(x)为减函数,
其值域为(1,+∞)知$\left\{\begin{array}{l}p=1\\{log_a}\frac{a-1}{a-3}=1,得a=2+\sqrt{3},p=1.\end{array}\right.$…(8分)
符合题意
综上①②:存在这样的实数p,a满足条件,$p=1,a=2+\sqrt{3}$…(9分)
(3)∵g(x)=-ax2+6(x-1)af(x)-5,$f(x)={log_a}\frac{1+x}{x-1}$
∴g(x)=-ax2+6x+1x∈[4,5]且a>0,a≠1
①当$\frac{3}{a}≤4⇒a≥\frac{3}{4},a≠1$时,函数g(x)在[4,5]上单调递减
所以g(x)max=g(4)=-16a+25…(11分)
②当$\frac{3}{a}≥5⇒0<a≤\frac{3}{5}$时,函数g(x)在[4,5]上单调递增
所以g(x)max=g(5)=-25a+31…(13分)
③当$\frac{3}{4}<a<\frac{3}{5}$时,函数g(x)在$[4,\frac{3}{a}]$上单调递增,在$[\frac{a}{3},5]$上单调递减
所以$g{(x)_{max}}=g(\frac{a}{3})=\frac{9}{a}+1$…15分
综上①②③,$g{(x)_{max}}=\left\{\begin{array}{l}-16a+25\begin{array}{l}{\;}&{a≥\frac{3}{4},a≠1}\end{array}\\ \frac{9}{a}+1\begin{array}{l}{\;}&{\;}&{\;}&{\frac{3}{5}<a<\frac{3}{4}}\end{array}\\-25a+31\begin{array}{l}{\;}&{0<a≤\frac{3}{5}}\end{array}\end{array}\right.$…(16分)
点评 本题考查函数的性质,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:填空题
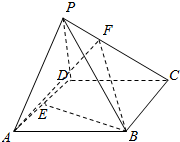 如图所示,P为?ABCD所在平面外一点,E为AD的中点,F为PC上一点,当PA∥平面EBF时,$\frac{PF}{FC}$=$\frac{1}{2}$.
如图所示,P为?ABCD所在平面外一点,E为AD的中点,F为PC上一点,当PA∥平面EBF时,$\frac{PF}{FC}$=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x∈R,且x≠-$\frac{π}{3}$} | B. | {x|x∈R,且x≠$\frac{5}{6}π$} | ||
| C. | {x|x∈R,且x≠kπ+$\frac{5}{6}$π,k∈Z} | D. | {x|x∈R,且x≠kπ-$\frac{5}{6}$π,k∈Z} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com