
【题目】已知函数f(x)=|x﹣1|+|x﹣a|.
(1)若a=2,解不等式f(x)≥2;
(2)已知f(x)是偶函数,求a的值.
【答案】
(1)解:当a=2时f(x)=|x﹣1|+|x﹣2|.
由f(x)≥2得|x﹣1|+|x﹣2|≥2.
(ⅰ)当x≤1,不等式化为1﹣x+2﹣x≥2.即x≤ ![]() .
.
(ⅱ)当1<x≤2,不等式化为x﹣1+2﹣x≥2不可能成立.
(iii)当x>2,不等式化为x﹣1+x﹣2≥2,即x≥2.5.
综上得,f(x)≥2的解集为{x|x≤ ![]() 或x≥2.5}
或x≥2.5}
(2)解:∵f(x)是偶函数,
∴f(﹣x)=f(x),
∴|﹣x﹣1|+|﹣x﹣a|=|x﹣1|+|x﹣a|.
∴a=﹣1
【解析】(1)分类讨论,去掉绝对值,即可解不等式f(x)≥2;(2)已知f(x)是偶函数,f(﹣x)=f(x),代入计算,即可求a的值.
【考点精析】认真审题,首先需要了解绝对值不等式的解法(含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号).


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】设函数y=f(x)是定义在(0,+∞)上的减函数,并且满足f(xy)=f(x)+f(y), ![]() .
.
(1)求f(1)的值;
(2)如果f(x)+f(2﹣x)<2,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直三棱柱ABC﹣A1B1C1中,AB=5,AC=4,BC=3,AA1=4,点D在AB上. 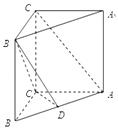
(1)若D是AB中点,求证:AC1∥平面B1CD;
(2)当 ![]() =
= ![]() 时,求二面角B﹣CD﹣B1的余弦值.
时,求二面角B﹣CD﹣B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() :
: ![]() ,其左右焦点为
,其左右焦点为![]()
![]() 及
及![]() ,过点
,过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
, ![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,
, ![]() 的中垂线与
的中垂线与![]() 轴和
轴和![]() 轴分别交于
轴分别交于![]() ,
, ![]() 两点,且
两点,且![]() 、
、![]() 、
、![]() 构成等差数列.
构成等差数列.
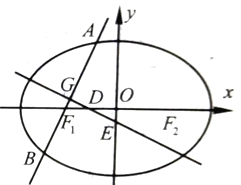
(1)求椭圆![]() 的方程;
的方程;
(2)记![]() 的面积为
的面积为![]() ,
, ![]() (
(![]() 为原点)的面积为
为原点)的面积为![]() .试问:是否存在直线
.试问:是否存在直线![]() ,使得
,使得![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (a>0).
(a>0).
(1)证明:当x>0时,f(x)在 ![]() 上是减函数
上是减函数 ![]() ,在上是增函数,并写出当x<0时f(x)的单调区间;
,在上是增函数,并写出当x<0时f(x)的单调区间;
(2)已知函数 ![]() ,函数g(x)=﹣x﹣2b,若对任意x1∈[1,3],总存在x2∈[1,3],使得g(x2)=h(x1)成立,求实数b的取值范围.
,函数g(x)=﹣x﹣2b,若对任意x1∈[1,3],总存在x2∈[1,3],使得g(x2)=h(x1)成立,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|0< ![]() ≤1},B={y|y=(
≤1},B={y|y=( ![]() )x , 且x<﹣1}
)x , 且x<﹣1}
(1)若集合C={x|x∈A∪B,且xA∩B},求集合C;
(2)设集合D={x|3﹣a<x<2a﹣1},满足A∪D=A,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com