
【题目】已知椭圆C: ![]() 的离心率
的离心率 ![]() ,且过点Q
,且过点Q ![]()
(1)求椭圆C的方程.
(2)椭圆C长轴两端点分别为A,B,点P为椭圆上异于A,B的动点,定直线x=4与直线PA,PB分别交于M,N两点,直线PA,PB的斜率分别为k1 , k2①证明 ![]() ;
;
②若E(7,0),过E,M,N三点的圆是否过x轴上不同于点E的定点?若经过,求出定点坐标;若不经过,请说明理由.
【答案】
(1)解:椭圆C: ![]() 焦点在x轴上,由e=
焦点在x轴上,由e= ![]() =
= ![]() ,即a=2c,
,即a=2c,
则b2=a2﹣c2=3c2,
由椭圆过点Q ![]() ,代入
,代入 ![]() ,解得:c=1,
,解得:c=1,
∴a=2,b= ![]() ,
,
∴椭圆的标准方程: ![]()
(2)解:①证明:由(1)得A(﹣2,0),B(2,0),设P(x,y),
则  ,
,
②设PA,PB的斜率分别为k1,k2,P(x0,y0),则k1k2=﹣ ![]() ,
,
可令PA:y=k1(x+2),则M(4,6k1),
PB:y=k2(x﹣2),则N(4,2k2),
又kEM=﹣ ![]() =﹣2k1,kEN=﹣
=﹣2k1,kEN=﹣ ![]() ,
,
∴kEMkEN=﹣1,
设圆过定点F(m,0),则 ![]()
![]() =﹣1,解得m=1或m=7(舍),
=﹣1,解得m=1或m=7(舍),
故过点E,M,N三点的圆是以MN为直径的圆,过x轴上不同于点E的定点F(1,0)
【解析】(1)由题意可知:e= ![]() =
= ![]() ,即a=2c,b2=a2﹣c2=3c2 , 将Q
,即a=2c,b2=a2﹣c2=3c2 , 将Q ![]() 代入椭圆方程,即可求得c的值,则求得a和b的值,即可求得椭圆C的方程;(2)①由(1)得A(﹣2,0),B(2,0),设P(x,y),由直线的斜率公式可知:则
代入椭圆方程,即可求得c的值,则求得a和b的值,即可求得椭圆C的方程;(2)①由(1)得A(﹣2,0),B(2,0),设P(x,y),由直线的斜率公式可知:则  ,②令PA:y=k1(x+2),则M(4,6k1),同理求得N(4,2k2),kEM=﹣
,②令PA:y=k1(x+2),则M(4,6k1),同理求得N(4,2k2),kEM=﹣ ![]() =﹣2k1 , kEN=﹣
=﹣2k1 , kEN=﹣ ![]() ,
, ![]()
![]() =﹣1,即可求得m=1,故过点E,M,N三点的圆是以MN为直径的圆,过x轴上不同于点E的定点F(1,0).
=﹣1,即可求得m=1,故过点E,M,N三点的圆是以MN为直径的圆,过x轴上不同于点E的定点F(1,0).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知公差不为0的等差数列{an}的前n项和为 ![]() ,若S3=a4+2,且a1 , a3 , a13成等比数列
,若S3=a4+2,且a1 , a3 , a13成等比数列
(1)求{an}的通项公式;
(2)设 ![]() ,求数列{bn}的前n项和为Tn .
,求数列{bn}的前n项和为Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(x﹣ ![]() )﹣sin(x﹣
)﹣sin(x﹣ ![]() ). (Ⅰ)判断函数f(x)的奇偶性,并给出证明;
). (Ⅰ)判断函数f(x)的奇偶性,并给出证明;
(Ⅱ)若θ为第一象限角,且f(θ+ ![]() )=
)= ![]() ,求cos(2θ+
,求cos(2θ+ ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从双曲线 ![]() =1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于点P,若M为线段FP的中点,O为坐标原点,则|MO|﹣|MT|与b﹣a的大小关系为( )
=1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于点P,若M为线段FP的中点,O为坐标原点,则|MO|﹣|MT|与b﹣a的大小关系为( )
A.|MO|﹣|MT|>b﹣a
B.|MO|﹣|MT|=b﹣a
C.|MP|﹣|MT|<b﹣a
D.不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若实数a,b,c满足loga3<logb3<logc3,则下列关系中不可能成立的( )
A.a<b<c
B.b<a<c
C.c<b<a
D.a<c<b
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为R,并满足以下条件:①对任意x∈R,有f(x)>0;②对任意x,y∈R,有f(xy)=[f(x)]y;③ ![]() .
.
(1)求证:f(x)在R上是单调增函数;
(2)若f(4x+a2x+1﹣a2+2)≥1对任意x∈R恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度υ(千米/小时)之间的函数关系为:y= ![]() (υ>0).
(υ>0).
(1)在该时段内,当汽车的平均速度υ为多少时,车流量最大?最大车流量为多少?(保留分数形式)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的部分图象如图所示,则y=f(x)的图象可由y=cos2x图象( )
)的部分图象如图所示,则y=f(x)的图象可由y=cos2x图象( ) 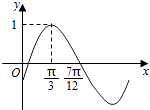
A.向右平移 ![]() 个长度单位
个长度单位
B.向左平移 ![]() 个长度单位
个长度单位
C.向右平移 ![]() 个长度单位
个长度单位
D.向左平移 ![]() 个长度单位
个长度单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆W: ![]() ,过原点O作直线l1交椭圆W于A,B两点,P为椭圆上异于A,B的动点,连接PA,PB,设直线PA,PB的斜率分别为k1 , k2(k1 , k2≠0),过O作直线PA,PB的平行线l2 , l3 , 分别交椭圆W于C,D和E,F.
,过原点O作直线l1交椭圆W于A,B两点,P为椭圆上异于A,B的动点,连接PA,PB,设直线PA,PB的斜率分别为k1 , k2(k1 , k2≠0),过O作直线PA,PB的平行线l2 , l3 , 分别交椭圆W于C,D和E,F.
(1)若A,B分别为椭圆W的左、右顶点,是否存在点P,使∠APB=90°?说明理由.
(2)求k1k2的值;
(3)求|CD|2+|EF|2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com