
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的参数方程为
的参数方程为 ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)求直线![]() 与曲线
与曲线![]() 的交点的直角坐标.
的交点的直角坐标.
科目:高中数学 来源: 题型:
【题目】我市某矿山企业生产某产品的年固定成本为![]() 万元,每生产千件该产品需另投入
万元,每生产千件该产品需另投入![]() 万元,设该企业年内共生产此种产品
万元,设该企业年内共生产此种产品![]() 千件,并且全部销售完,每千件的销售收入为
千件,并且全部销售完,每千件的销售收入为![]() 万元,且
万元,且
(Ⅰ)写出年利润![]() (万元)关于产品年产量
(万元)关于产品年产量![]() (千件)的函数关系式;
(千件)的函数关系式;
(Ⅱ)问:年产量![]() 为多少千件时,该企业生产此产品所获年利润最大?
为多少千件时,该企业生产此产品所获年利润最大?
注:年利润=年销售收入-年总成本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),已知图中从左到右前三个小组的频率分别为 0.1,0.3,0.4,第一小组的频数为 5. 
(1)求第四小组的频率;
(2)若次数在 75 次以上(含75 次)为达标,试估计该年级学生跳绳测试的达标率.
(3)在这次测试中,一分钟跳绳次数的中位数落在哪个小组内?试求出中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将正方形ABCD沿对角线BD折成直二面角A﹣BD﹣C,有如下四个结论:
①AC⊥BD;
②△ACD是等边三角形;
③AB与平面BCD成60°的角;
④AB与CD所成的角为60°;
其中正确结论是(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的参数方程为
的参数方程为 ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)求直线![]() 与曲线
与曲线![]() 的交点的直角坐标.
的交点的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某重点高中拟把学校打造成新型示范高中,为此制定了学生“七不准”,“一日三省十问”等新的规章制度.新规章制度实施一段时间后,学校就新规章制度随机抽取部分学生进行问卷调查,调查卷共有10个问题,每个问题10分,调查结束后,按分数分成5组:[50,60),60,70),[70,80),[80,90),[90,100],并作出频率分布直方图与样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据). 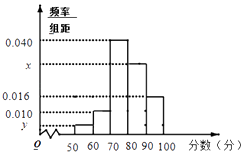
(1)求样本容量n和频率分布直方图中的x、y的值;
(2)在选取的样本中,从分数在70分以下的学生中随机抽取2名学生进行座谈会,求所抽取的2名学生中恰有一人得分在[50,60)内的概率.
5 | 3 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com