
已知一个口袋中装有 个红球(
个红球( 且
且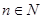 )和
)和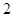 个白球,从中有放回地连续摸三次,每次摸出两个球,若两个球颜色不同则为中奖,否则不中奖.
个白球,从中有放回地连续摸三次,每次摸出两个球,若两个球颜色不同则为中奖,否则不中奖.
(1)当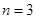 时,设三次摸球中(每次摸球后放回)中奖的次数为
时,设三次摸球中(每次摸球后放回)中奖的次数为 ,求的
,求的 分布列;
分布列;
(2)记三次摸球中(每次摸球后放回)恰有两次中奖的概率为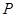 ,当
,当 取多少时,
取多少时,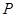 最大.
最大.
(1)分布列见解析(2)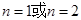
【解析】本题是一个在等可能性事件基础上的独立重复试验问题,体现了不同概型的综合.第Ⅲ小题中的函数是三次函数,运用了导数求三次函数的最值
(1)本题是一个等可能事件的概率,若n=3,一次摸奖中奖的概率p=5/9 ,三次摸奖是独立重复试验,然后利用n次独立重复试验中恰好发生k次的概率公式进行求解即可;
(2)设每次摸奖中奖的概率为p,则三次摸奖(每次摸奖后放回),恰有一次中奖的概率为P为P=P3(1)=C31•p•(1-p)2=3p3-6p2+3p,当p= 时,P取得最大值.得到n的值.
时,P取得最大值.得到n的值.
解:(1)当 时,每次摸出两个球,中奖的概率
时,每次摸出两个球,中奖的概率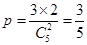
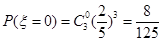 ;
;
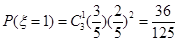 ;
;
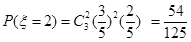 ;
;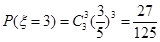 ;
;
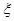 分布列为:
分布列为:

(2)设每次摸奖中奖的概率为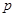 ,则三次摸球(每次摸奖后放回)恰有两次中奖的概率为:
,则三次摸球(每次摸奖后放回)恰有两次中奖的概率为: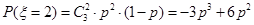 ,
,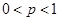 ,
,
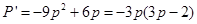 ,知在
,知在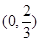 上
上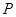 为增函数,在
为增函数,在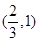 上
上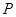 为减函数,当
为减函数,当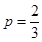 时
时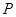 取得最大值.
取得最大值.
又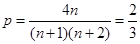 ,
, 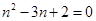 解得
解得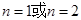 .
.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:浙江省瑞安中学2011-2012学年高二下学期期末考试数学理科试题 题型:044
已知一个口袋中装有n个红球(n≥1且n∈N)和2个白球,从中有放回地连续摸三次,每次摸出两个球,若两个球颜色不同则为中奖,否则不中奖.
(1)当n=3时,设三次摸球中(每次摸球后放回)中奖的次数为ξ,求的ξ分布列;
(2)记三次摸球中(每次摸球后放回)恰有两次中奖的概率为P,当n取多少时,P最大.
查看答案和解析>>
科目:高中数学 来源:2014届江西省景德镇市高二下学期期末考试理科数学试卷(解析版) 题型:解答题
在一个口袋中装有12个大小相同的黑球、白球和红球。已知从袋中任意摸出2个球,至少得到一个黑球的概率是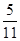 。
。
求:(1)袋中黑球的个数;
(2)从袋中任意摸出3个球,至少得到2个黑球的概率。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省景德镇市昌江一中高三(上)第三次月考数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com