
【题目】已知数列{an}满足:a1=1,a2=2,且an+1=2an+3an﹣1(n≥2,n∈N+).
(1)设bn=an+1+an(n∈N+),求证{bn}是等比数列;
(2)(i)求数列{an}的通项公式;
(ii)求证:对于任意n∈N+都有 ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() <
< ![]() 成立.
成立.
【答案】
(1)证明:已知数列{an}满足:a1=1,a2=2,且an+1=2an+3an﹣1(n≥2,n∈N+).
则:an+1+an=3(an+an﹣1)
即: ![]() ,
,
所以: ![]() ,
,
数列{bn}是等比数列.
(2)解:(i)由于数列{bn}是等比数列.
则: ![]() ,
,
整理得: ![]()
所以: ![]()
则: ![]() 是以(
是以( ![]() )为首项,﹣1为公比的等比数列.
)为首项,﹣1为公比的等比数列.
所以: ![]()
求得: ![]()
(ii)由于: ![]() ,
,
所以: ![]() ,
,
则:(1)当n为奇数时, ![]() ,
,
当n为偶数时, ![]() ,
,
所以: ![]() =
= ![]() …+
…+ ![]() +
+ ![]()
![]() ,
,
所以:n∈k时,对任意的k都有 ![]() 恒成立
恒成立
【解析】(1)利用已知条件对已知的数列关系式进行恒等变形,进一步的出数列是等比数列.(2)(i)根据(1)的结论进一步利用恒等变换,求出数列的通项公式.(ii)首先分奇数和偶数分别写出通项公式,进一步利用放缩法进行证明.
【考点精析】本题主要考查了等比关系的确定和数列的前n项和的相关知识点,需要掌握等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断;数列{an}的前n项和sn与通项an的关系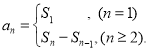 才能正确解答此题.
才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图所示的空间几何体中,底面四边形![]() 为正方形,
为正方形, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)求二面角![]() 的大小;
的大小;
(2)若在平面![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,试通过计算说明点
,试通过计算说明点![]() 的位置.
的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司在迎新年晚会上举行抽奖活动,有甲、乙两个抽奖方案供员工选择.
方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率均为![]() ,第一次抽奖,若未中奖,则抽奖结束,若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖。规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,则获得1000元;若未中奖,则所获得奖金为0元.
,第一次抽奖,若未中奖,则抽奖结束,若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖。规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,则获得1000元;若未中奖,则所获得奖金为0元.
方案乙:员工连续三次抽奖,每次中奖率均为![]() ,每次中奖均可获得奖金400元.
,每次中奖均可获得奖金400元.
(1)求某员工选择方案甲进行抽奖所奖金![]() (元)的分布列;
(元)的分布列;
(2)试比较某员工选择方案乙与选择方案甲进行抽奖,哪个方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料,生产1扯皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如表所示:
| A | B | C |
甲 | 4 | 8 | 3 |
乙 | 5 | 5 | 10 |
现有A种原料200吨,B种原料360吨,C种原料300吨,在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车品乙种肥料,产生的利润为3万元、分别用x,y表示计划生产甲、乙两种肥料的车皮数.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲、乙两种肥料,求出此最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
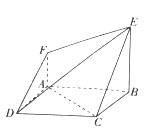
【题目】如图,在三棱柱ABC﹣A1B1C1中,AA1⊥底面ABC,∠BAC=90°,AB=AC=2, ![]() .M,N分别为BC和CC1的中点,P为侧棱BB1上的动点.
.M,N分别为BC和CC1的中点,P为侧棱BB1上的动点. 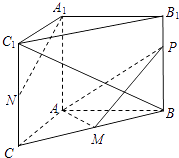
(1)求证:平面APM⊥平面BB1C1C;
(2)若P为线段BB1的中点,求证:A1N∥平面APM;
(3)试判断直线BC1与平面APM是否能够垂直.若能垂直,求PB的值;若不能垂直,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设已知双曲线![]() 的焦点为
的焦点为![]() ,过
,过![]() 的直线
的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点.
两点.
(1)若直线![]() 的倾斜角为
的倾斜角为![]() ,且
,且![]() ,求
,求![]() ;
;
(2)若![]() ,椭圆
,椭圆![]() 上两个点
上两个点![]() 满足:
满足: ![]() 三点共线且
三点共线且![]() ,求四边形
,求四边形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC, 点D是AB的中点.
(Ⅰ)求证:CD⊥平面A1ABB1;
(Ⅱ)求证:AC1∥平面CDB1;
(Ⅲ)线段AB上是否存在点M,使得A1M⊥平面CDB1?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在区间![]() 上的函数
上的函数![]() 和
和![]() ,如果对任意
,如果对任意![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 在区间
在区间![]() 上可被
上可被![]() 替代,
替代, ![]() 称为“替代区间”.给出以下问题:
称为“替代区间”.给出以下问题:
①![]() 在区间
在区间![]() 上可被
上可被![]() 替代;
替代;
②如果![]() 在区间
在区间![]() 可被
可被![]() 替代,则
替代,则![]() ;
;
③设![]() ,则存在实数
,则存在实数![]() 及区间
及区间![]() , 使得
, 使得![]() 在区间
在区间![]() 上被
上被![]() 替代.
替代.
其中真命题是
A. ①②③ B. ②③ C. ①③ D. ①②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com