
| A. | 命题:?x∈R,x2≠x的否定是:?x0∈R,使得x02≠x | |
| B. | 命题:若x≥2且y≥3,则x+y≥5的否命题为:若x<2且y<3,则x+y<5 | |
| C. | 若ω=1是函数f(x)=cosωx在区间[0,π]上单调递减的充分不必要条件 | |
| D. | 命题:?x0∈R,x02+a<0为假命题,则实数a的取值范围是a>0 |
分析 利用命题的否定判断A的正误;四种命题的逆否关系判断B的正误;充要条件判断C的正误;命题的真假判断D的正误;
解答 解:对于A,命题:?x∈R,x2≠x的否定是:?x0∈R,使得x02≠x0,不满足命题的否定形式,所以不正确;
对于B,命题:若x≥2且y≥3,则x+y≥5的否命题为:若x<2且y<3,则x+y<5,不满足否命题的形式,所以不正确;
对于C,若ω=1是函数f(x)=cosx在区间[0,π]上单调递减的,而函数f(x)=cosωx在区间[0,π]上单调递减的,ω≤1,所以ω=1是函数f(x)=cosωx在区间[0,π]上单调递减的充分不必要条件,正确.
对于D,命题:?x0∈R,x02+a<0为假命题,则命题:a≥0,?x∈R,x2+a≥0是真命题;所以,命题:?x0∈R,x02+a<0为假命题,则实数a的取值范围是a>0,不正确;
故选:C.
点评 本题考查命题的真假的判断与应用,基本知识的考查.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -1 | C. | $1+2\sqrt{3}$ | D. | $1-2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一天,小亮看到家中的塑料桶中有一个竖直放置的玻璃杯,桶子和玻璃杯的形状都是圆柱形,桶口的半径是杯口半径的2倍,其主视图如左图所示.小亮决定做个试验:把塑料桶和玻璃杯看作一个容器,对准杯口匀速注水,注水过程中杯子始终竖直放置,则下列能反映容器最高水位h与注水时间t之间关系的大致图象是( )
一天,小亮看到家中的塑料桶中有一个竖直放置的玻璃杯,桶子和玻璃杯的形状都是圆柱形,桶口的半径是杯口半径的2倍,其主视图如左图所示.小亮决定做个试验:把塑料桶和玻璃杯看作一个容器,对准杯口匀速注水,注水过程中杯子始终竖直放置,则下列能反映容器最高水位h与注水时间t之间关系的大致图象是( )| A. |  | B. |  | ||
| C. |  | D. | 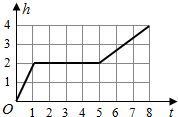 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 9 | C. | -3 | D. | ±3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com