
已知![]() ,其中
,其中![]() 是无理数,且
是无理数,且![]() ,
,![]()
(1)当![]() 时, 求
时, 求![]() 的单调区间、极值;
的单调区间、极值;
(2)求证:在(1)的条件下,![]() ;
;
(3)是否存在实数![]() ,使
,使![]() 的最小值是
的最小值是![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由
的值;若不存在,说明理由
(1) ![]() 的的单调递减区间为(0,1);单调递增区间为(1,e);
的的单调递减区间为(0,1);单调递增区间为(1,e);![]() 的极小值为
的极小值为![]()
(3) ![]()
(1)![]() 当
当![]() 时,
时,![]()
![]() , 1分
, 1分
∴当![]() 时,
时,![]() ,此时
,此时![]() 单调递减
单调递减
当![]() 时,
时,![]() ,此时
,此时![]() 单调递增 …………………………………3分
单调递增 …………………………………3分
![]() 的的单调递减区间为(0,1);单调递增区间为(1,e);
的的单调递减区间为(0,1);单调递增区间为(1,e);
![]() 的极小值为
的极小值为![]() ………………………………………………4分
………………………………………………4分
(2)由(1)知![]() 在
在![]() 上的最小值为1, ……………………………………5分
上的最小值为1, ……………………………………5分
令![]() ,
,![]()
![]() , ………………………6分
, ………………………6分
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增 …………………………………7分
上单调递增 …………………………………7分
∴![]() w
w
∴在(1)的条件下,![]() …………………………………………………8分
…………………………………………………8分
(1)假设存在实数![]() ,使
,使![]() (
(![]() )有最小值
)有最小值![]() ,
,
![]() ……………………………………………………9分
……………………………………………………9分
①当![]() 时,
时,
![]() ,
,
![]()
![]() 在
在![]() 上单调递增,此时
上单调递增,此时![]() 无最小值. …10分
无最小值. …10分
②当![]() 时,
时,
若![]() ,故
,故![]() 在
在![]() 上单调递减,
上单调递减,
若![]() ,故
,故![]() 在
在![]() 上单调递增.
上单调递增.
![]() ,得
,得![]() ,满足条件. ……………………………12分
,满足条件. ……………………………12分
③当![]() 时,
时,
![]() ,
,![]()
![]() 在
在![]() 上单调递减,
上单调递减,
![]() (舍去),
(舍去),
所以,此时![]() 无最小值. ……13分w.w.w.k.s.5.u.c.o.m
无最小值. ……13分w.w.w.k.s.5.u.c.o.m ![]()
![]()
综上,存在实数![]() ,使得当
,使得当![]() 时
时![]() 的最小值是
的最小值是![]() ……………………14分
……………………14分
(3)法二:假设存在实数![]() ,使
,使![]()
![]() 的最小值是
的最小值是![]() ,
,
故原问题等价于:不等式![]() 对
对![]() 恒成立,求“等号”取得时实数a的值.
恒成立,求“等号”取得时实数a的值.
即不等式![]() 对
对![]() 恒成立,求“等号”取得时实数a的值.
恒成立,求“等号”取得时实数a的值.
设![]() 即
即![]() ,
,![]() ………………10分
………………10分
又![]() ……………………………11分
……………………………11分
令![]()
当![]() ,
,![]() ,则
,则![]() 在
在![]() 单调递增;
单调递增;
当![]() ,
,![]() ,则
,则![]() 在
在![]() 单调递减. ……………………13分
单调递减. ……………………13分
故当![]() 时,
时,![]() 取得最大值,其值是
取得最大值,其值是![]() .
.
故![]()
综上,存在实数![]() ,使得当
,使得当![]() 时
时![]() 的最小值是
的最小值是![]() .……………………14分
.……………………14分


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
(本小题满分12分)
已知![]() ,其中
,其中![]() 是无理数,且
是无理数,且![]() ,
, ![]() .
.
(1)若![]() 时, 求
时, 求![]() 的单调区间、极值;
的单调区间、极值;
(2)求证:在(1)的条件下,![]() ;
;
(3)是否存在实数![]() ,使
,使![]() 的最小值是
的最小值是![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
已知![]() ,其中
,其中![]() 是无理数,且
是无理数,且![]() ,
, ![]() .
.
(1)若![]() 时, 求
时, 求![]() 的单调区间、极值;
的单调区间、极值;
(2)求证:在(1)的条件下,![]() ;
;
(3)是否存在实数![]() ,使
,使![]() 的最小值是
的最小值是![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省肇庆市高二(下)期末数学试卷(文科)(解析版) 题型:解答题
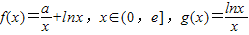 ,其中e是无理数,a∈R.
,其中e是无理数,a∈R.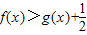 ;
;查看答案和解析>>
科目:高中数学 来源:2010年河南省焦作市高考数学二模试卷(理科)(解析版) 题型:解答题
 ,其中e是无理数,a∈R.
,其中e是无理数,a∈R. ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com