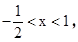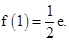试题分析:f′(x)=e
x[x
2+(a+2)x+a+2]
(1)当a=0时,f(x)=(x
2+2)e
x,f′(x)=e
x(x
2+2x+2),f(1)=3e,
f′(1)=5e,
∴函数f(x)的图象在点A(1,f(1))处的切线方程为y-3e=5e(x-1),即5ex-y-2e=0.
(2)f′(x)=e
x[x
2+(a+2)x+a+2],
考虑到e
x>0恒成立且x
2系数为正.
∴f(x)在R上单调等价于x
2+(a+2)x+a+2≥0恒成立.
∴(a+2)
2-4(a+2)≤0.
解得-2≤a≤2,即a的取值范围是[-2,2],
(3)当

时,f(x)=

,
f′(x)=
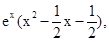
令f′(x)=0,得
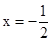
或x=1.
令f′(x)>0,得
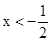
或x>1.
令f′(x)<0,得
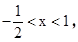
x,f′(x),f(x)的变化情况如下表
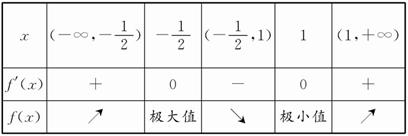
所以,函数f(x)的极小值为
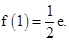
点评:注意极值与最值的区别和联系:最大值是极值与边界值中最大的函数值,最小值是极值与边界值中最小的函数值

 时,求函数f(x)的极小值.
时,求函数f(x)的极小值.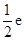
 时,f(x)=
时,f(x)= ,
,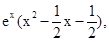
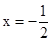 或x=1.
或x=1.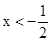 或x>1.
或x>1.