
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,左顶点为
,左顶点为![]() ,离心率为
,离心率为![]() ,点
,点![]() 是椭圆上的动点,
是椭圆上的动点,![]() 的面积的最大值为
的面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() ,线段
,线段![]() 的中垂线为
的中垂线为![]() .若直线
.若直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,求
,求![]() 的最小值.
的最小值.
 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:
【题目】给出下列说法:
①“![]() ”是“
”是“![]() ”的充分不必要条件;
”的充分不必要条件;
②定义在![]() 上的偶函数
上的偶函数![]() 的最大值为30;
的最大值为30;
③命题“![]() ,
,![]() ”的否定形式是“
”的否定形式是“![]() ,
,![]() ”.其中正确说法的个数为
”.其中正确说法的个数为
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年国际乒联总决赛在韩国仁川举行,比赛时间为12月13﹣12月16日,在男子单打项目,中国队准备选派4人参加.已知国家一线队共6名队员,二线队共4名队员.
(1)求恰好有3名国家一线队队员参加比赛的概率;
(2)设随机变量![]() 表示参加比赛的国家二线队队员的人数,求
表示参加比赛的国家二线队队员的人数,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种体育比赛的规则是:进攻队员与防守队员均在安全线![]() 的垂线
的垂线![]() 上(
上(![]() 为垂足),且分别位于距
为垂足),且分别位于距![]() 为
为![]() 和
和![]() 的点
的点![]() 和点
和点![]() 处,进攻队员沿直线
处,进攻队员沿直线![]() 向安全线跑动,防守队员沿直线方向拦截,设
向安全线跑动,防守队员沿直线方向拦截,设![]() 和
和![]() 交于点
交于点![]() ,若在
,若在![]() 点,防守队员比进攻队员先到或同时到,则进攻队员失败,已知进攻队员速度是防守队员速度的两倍,且他们双方速度不变,问进攻队员的路线
点,防守队员比进攻队员先到或同时到,则进攻队员失败,已知进攻队员速度是防守队员速度的两倍,且他们双方速度不变,问进攻队员的路线![]() 应为什么方向才能取胜?
应为什么方向才能取胜?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是总体的一个样本频率分布直方图,且在![]() 内频数为8.求:
内频数为8.求:
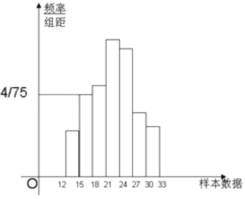
(1)求样本容量;
(2)若在![]() 内的小矩形面积为0.06,求在
内的小矩形面积为0.06,求在![]() 内的频数和样本在
内的频数和样本在![]() 内的频率.
内的频率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C: ![]() ,直线l过点
,直线l过点![]() .
.

(1)若直线l与圆心C的距离为1,求直线l的方程;
(2)若直线l与圆C交于M,N两点,且![]() ,求以MN为直径的圆的方程;
,求以MN为直径的圆的方程;
(3)设直线![]() 与圆C交于A,B两点,是否存在实数a,使得直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,说明理由.
与圆C交于A,B两点,是否存在实数a,使得直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com