Question

（1）若方程7x²-（k+13）x+k²-k-2=0的两根分别在（0，1）和（1，2）内，求k的取值范围．
（2）已知方程x²+（m-2）x+2m-1=0有且只有一个实根在（0，1）内，求m的取值范围．

Answer 1

分析：（1）设出方程对应的函数，据方程的根的分布画出函数的图象，结合图象知函数在x=0时为正，x=1时为负，x=2时为正．
（2）设出方程对应的函数，据方程的根的分布画出函数的图象，结合图象知函数在x=0及x=1处的函数值异号或判别式为0且对称轴在（0，1）内．

解答：解：（1）令f（x）=7x²-（k+13）x+k²-k-2
∵方程7x²-（k+13）x+k²-k-2=0的两根分别在（0，1）和（1，2）内
∴f（x）的图象如下：

∴

f(0)＞0 f(1)＜0 f(2)＞0

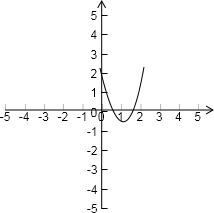
即

k2-k-2＞0 k2-2k-8＜ k2-3k＞0

0
解得-2＜k＜-1或3＜k＜4
（2）令g（x）=x²+（m-2）x+2m-1
∵方程x²+（m-2）x+2m-1=0有且只有一个实根在（0，1）内
∴g（x）的图象如下：

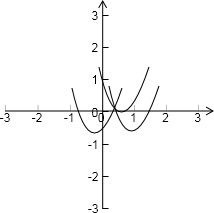(2m-1)(3m-2)＜0或

△=0 0＜ 2-m 2 ＜1

解得

1

2

＜m＜

2

3

或m=6-2

7

点评：本题考查解二次方程实根分布的方法：画出对应函数的图象，结合图象写出系数满足的条件．