
分析 考虑函数g(x)=x3-3x,求出导数,求得最值,再考虑h(x)=x3-3x-t+1的图象为g(x)上下平移的结果,而f(x)就是h(x)负的部分翻到x轴上面得到的图象,讨论h(0)≥0,h(0)≤0,求出f(x)的最大值,解方程即可得到所求.
解答 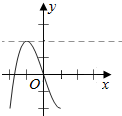 解:观察函数g(x)=x3-3x,
解:观察函数g(x)=x3-3x,
g′(x)=3x2-3,表明g(x)在[-2,-1]递增,在[-1,1]递减,
g(-2)=-2,g(1)=-2,最大值g(-1)=2,
容易画出g(x)图象如右,
h(x)=x3-3x-t+1就是g(x)上下平移的结果,
f(x)就是h(x)负的部分翻到x轴上面得到的图象,
考察h(x)①h(0)≥0,则h(x)最大值的绝对值大于h(x)最小值的绝对值,
因此h(0)=-t+1≥0,f(x)最大值在x=-1处取得,与h(x)最大值相等,
h(-1)=-t+3=2,解得t=1;
②h(0)≤0,则h(x)最大值的绝对值小于h(x)最小值的绝对值,
因此h(0)=-t+1≤0,f(x)最大值在x=-2或者x=1处取得,
与h(x)最小值的相反数相等.h(1)=-t-1=-2,解得t=1.
综上可得t=1.
故答案为:1.
点评 本题考查函数的最值的求法,考查函数的奇偶性和单调性的应用,考查运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②③④ | B. | ①③ | C. | ② | D. | ④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com