【答案】
分析:(1)根据指数的运算性质将原方程化为4•(2
x)
2-4•2
x-24=0,将2
x看成一个整体,则方程可转化为一个二次型方程,解方程并对所得方程的根结合指数函数的性质进行判断,即可得到答案.
(2)根据对数运算性质,我们可将原方程转化为一个分式方程的形式,进而求出满足条件的答案.
(3)根据对数函数的单调性,我们可将原不等式转化为一个关于x的一元一次不等式,解不等式即可得到答案.
解答:解:(1)若4
x+1-4×2
x-24=0
即4•(2
x)
2-4•2
x-24=0
即(2
x)
2-2
x-6=0
即2
x=3,或2
x=-2(舍去)
故x=log
23
(2)若lg(x
2-x-2)-lg(x+1)-lg2=0
则

=0
即

=0
即

=1
故x=4
(3)若

则0<x-2≤2
解得2<x≤4
故不等式的解集为(2,4]
点评:本题考查的知识点是指数函数单调性的应用,及对数函数单调性的应用,其中在解答(3)时,一定要注意真数部分大于0的限制,本题易忽略此点而错解为(-∞,2]

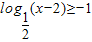 .
. =0
=0 =0
=0 =1
=1


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案