
【题目】求和:Sn= ![]() +
+ ![]() +…+
+…+ ![]() ,并用数学归纳法证明.
,并用数学归纳法证明.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f ( x)=ax3+bx2+cx+d 的图象如图所示,则 ![]() 的取值范围是( )
的取值范围是( ) 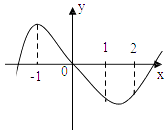
A.(﹣ ![]() ,
, ![]() ?)
?)
B.(﹣ ![]() ,1)
,1)
C.(﹣ ![]() ,
, ![]() )
)
D.(﹣ ![]() ,1)
,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱ABC﹣A1B1C1的直观图和三视图如图所示,E是棱CC1上一点. 
(1)若CE=2EC1 , 求三棱锥E﹣ACB1的体积.
(2)若E是CC1的中点,求C到平面AEB1的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知位置向量 ![]() =(log2(m2+3m﹣8),log2(2m﹣2)),
=(log2(m2+3m﹣8),log2(2m﹣2)), ![]() =(1,0),若以OA、OB为邻边的平行四边形OACB的顶点C在函数y=
=(1,0),若以OA、OB为邻边的平行四边形OACB的顶点C在函数y= ![]() x的图象上,则实数m= .
x的图象上,则实数m= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盒子中有大小相同的球6个,其中标号为1的球2个,标号为2的球3个.标号为3的球1个,第一次从盒子中任取1个球,放回后第二次再任取1个球 (假设取到每个球的可能性都相同).记第一次与第二次取到球的标号之和为ξ.
(1)求随机变量ξ的分布列:
(2)求随机变量ξ的期望Eξ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com