Question

已知三个数a、b、c成等比数列，其积为8，又a、b、c-1成等差数列，求这三个数组成的数列．

Answer 1

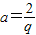
【答案】分析：由性质可得b=2，即，b=2，c=2q，再由等差数列的性质可得关于q的方程，解之可得．
解答：解：由题意可得设，c=bq，
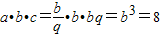
∴．解得b=2．
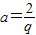
即，b=2，c=2q  …（2分）
又又a、b、c-1成等差数列，∴2b=a+（c-1），
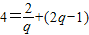
∴．∴2q²-5q+2=0．∴q=2或． …（4分）
当q=2时，a=1，b=2，c=4；
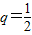
当时，a=4，b=2，c=1．
即所求数列为1、2、4或4、2、1． …（6分）
点评：本题考查等差数列和等比数列的综合应用，涉及一元二次方程的解法和分类讨论的思想，属中档题．