
解答题
已知函数f(x)=x2-1(x≥1)的曲线为C1,曲线C2与C1关于直线y=x对称.
(1)求曲线C2的方程y=g(x);
(2)设函数y=g(x)的定义域为M,x1,x2∈M,且x1≠x2,求证:|g(x1)-g(x2)|<|x1-x2|:
(3)设A、B为曲线C2上任意不同两点,证明直线AB与直线y=x必相交.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
已知函数f(x)=m(x+![]() )的图象与函数h(x)=
)的图象与函数h(x)=![]() (x+
(x+![]() )+2的图象关于点A(0,1)对称.
)+2的图象关于点A(0,1)对称.
(1)求m的值;
(2)若g(x)=f(x)+![]() 在区间(0,2]上为减函数,求实数a的取值范围.
在区间(0,2]上为减函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2004全国各省市高考模拟试题汇编(天利38套)·数学 题型:044
已知函数f(x)的图像与函数h(x)=x+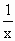 +2的图像关于点A(0,1)对称.
+2的图像关于点A(0,1)对称.
(1)求f(x)的解析式;
(2)(文)若g(x)=f(x)·x+ax,且g(x)在区间(0,2]上为减函数,求实数a的取值范围;
(理)若g(x)=f(x)+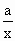 ,且g(x)在区间(0,2]上为减函数,求实数a的取值范围.
,且g(x)在区间(0,2]上为减函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
已知函数f(x)=![]() .
.
(1)求f(x)的定义域;
(2)用定义判断f(x)的奇偶性;
(3)在[-π,π]上作出f(x)的图象;
(4)指出f(x)的最小正周期及单调递增区间.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
已知函数f(x)的定义域是R,对任意x、y∈R,都有f(x+y)=f(x)+f(y),且x>0时,f(x)<0,f(1)=-2,求f(x)在[-3,3]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源:中学教材标准学案 数学 高二上册 题型:047
解答题
已知函数f(x)=x3-x+c定义在区间[0,1]上,x1、x2∈[0,1]且x1≠x2.
求证:(1)f(0)=f(1);
(2)|f(x2)-f(x1)|<2|x2-x1|;
(3)|f(x2)-f(x1)|<1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com