
ЁОЬтФПЁПгУвЛИіЦНУцШЅНижБСЂЗХжУЕФдВжљЃЌЕУдВжљЕФЯТАыВПЗжШчЭМЃЌЦфжа![]() ЮЊНиУцЕФзюЕЭЕуЃЌ
ЮЊНиУцЕФзюЕЭЕуЃЌ![]() ЮЊНиУцЕФзюИпЕуЃЌ
ЮЊНиУцЕФзюИпЕуЃЌ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() жаЕуЃЌ
жаЕуЃЌ![]() ЮЊНиУцБпНчЩЯШЮвтвЛЕуЃЌзї
ЮЊНиУцБпНчЩЯШЮвтвЛЕуЃЌзї![]() ДЙжБдВжљЕзУцгкЕу
ДЙжБдВжљЕзУцгкЕу![]() ЃЌ
ЃЌ![]() ДЙжБдВжљгкЕзУцгкЕу
ДЙжБдВжљгкЕзУцгкЕу![]() ЃЌ
ЃЌ![]() ДЙжБдВжљгкЕзУцгкЕу
ДЙжБдВжљгкЕзУцгкЕу![]() ЃЌдВжљЕзУцдВаФЮЊ
ЃЌдВжљЕзУцдВаФЮЊ![]() ЁЃвбжЊ
ЁЃвбжЊ![]() ЮЊЕзУцжБОЖЃЌ
ЮЊЕзУцжБОЖЃЌ![]() дквд
дквд![]() ЮЊжБОЖЕФдВжмЩЯЃЌ
ЮЊжБОЖЕФдВжмЩЯЃЌ![]() ДЙжБЕзУцЃЌ
ДЙжБЕзУцЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌвд
ЃЌвд![]() ЮЊдЕуЃЌ
ЮЊдЕуЃЌ![]() ЮЊ
ЮЊ![]() жсе§ЗНЯђЃЌдВжљЕзУцЮЊ
жсе§ЗНЯђЃЌдВжљЕзУцЮЊ![]() ЦНУцЃЌ
ЦНУцЃЌ![]() ЮЊ
ЮЊ![]() жсе§ЗНЯђНЈСЂПеМфжБНЧзјБъЯЕЃЌЩшЕу
жсе§ЗНЯђНЈСЂПеМфжБНЧзјБъЯЕЃЌЩшЕу![]() ЁЃ
ЁЃ


ЃЈ1ЃЉЧѓЕу![]() ЕФзјБъЃЌВЂЧѓГі
ЕФзјБъЃЌВЂЧѓГі![]() гы
гы![]() жЎМфТњзуЕФЙиЯЕЪНЃЛ
жЎМфТњзуЕФЙиЯЕЪНЃЛ
ЃЈ2ЃЉШ§ЪгЭМЪЧНтОіСЂЬхМИКЮЮЪЬтЪБЕФгааЇЙЄОпЃЌНЋдВжљЯТАыВПЗждк![]() ЦНУцЩЯЕФЭЖгАзїЮЊжїЪгЭМЃЌдк
ЦНУцЩЯЕФЭЖгАзїЮЊжїЪгЭМЃЌдк![]() ЦНУцЩЯЕФЭЖгАзїЮЊИЉЪгЭМЃЛдкЗНПђжазїГіжїЪгЭМЃЌВЂЫЕУїРэгЩЃЛдйЧѓГізѓЪгЭМЫљЮЇЧјгђЕФУцЛ§ЃЛ
ЦНУцЩЯЕФЭЖгАзїЮЊИЉЪгЭМЃЛдкЗНПђжазїГіжїЪгЭМЃЌВЂЫЕУїРэгЩЃЛдйЧѓГізѓЪгЭМЫљЮЇЧјгђЕФУцЛ§ЃЛ
ЃЈ3ЃЉХаЖЯНиУцЕФБпНчЪЧЪВУДЧњЯпЃЌВЂжЄУї.дйжИГіНиУцЕФУцЛ§ЃЈВЛашвЊжЄУїЃЉ
ЁОД№АИЁПЃЈ1ЃЉ![]() ;
;![]() ЃЈ2ЃЉжїЪгЭММћНтЮі;
ЃЈ2ЃЉжїЪгЭММћНтЮі; ![]() ЃЈ3ЃЉЭждВ,жЄУїМћНтЮі;
ЃЈ3ЃЉЭждВ,жЄУїМћНтЮі; ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОн![]() ДЙжБдВжљгкЕзУцгкЕу
ДЙжБдВжљгкЕзУцгкЕу![]() ,МДПЩЕУ
,МДПЩЕУ![]() ЕФзјБъ;гЩгк
ЕФзјБъ;гЩгк![]() ЮЛгкЕзУцЕФдВжмЩЯ,НсКЯдВЕФЗНГЬМДПЩЕУ
ЮЛгкЕзУцЕФдВжмЩЯ,НсКЯдВЕФЗНГЬМДПЩЕУ![]() гы
гы![]() жЎМфТњзуЕФЙиЯЕ.
жЎМфТњзуЕФЙиЯЕ.
ЃЈ2ЃЉИљОнМИКЮЬх,ПЩЕУжїЪгЭМ;ЛГізѓЪгЭМ,МДПЩЧѓЕУзѓЪгЭМЮЇГЩЭМаЮЕФУцЛ§.
ЃЈ3ЃЉИљОнЦНУцНидВжљаЮГЩНиУцаджЪПЩжЊЫљЕУНиУцЮЊЭждВ.ИљОнЭждВЕФУцЛ§ЧѓЗЈМДПЩЕУНиУцУцЛ§.
ЃЈ1ЃЉвд![]() ЮЊдЕу,
ЮЊдЕу,![]() ЮЊ
ЮЊ![]() жсе§ЗНЯђ,дВжљЕзУцЮЊ
жсе§ЗНЯђ,дВжљЕзУцЮЊ![]() ЦНУц,
ЦНУц,![]() ЮЊ
ЮЊ![]() жсе§ЗНЯђНЈСЂПеМфжБНЧзјБъЯЕ
жсе§ЗНЯђНЈСЂПеМфжБНЧзјБъЯЕ
вђЮЊ![]() ДЙжБдВжљгкЕзУцгкЕу
ДЙжБдВжљгкЕзУцгкЕу![]() ,Чв
,Чв![]()
Ыљвд![]()
вђЮЊЕзУцЪЧвд![]() ЮЊдВаФЕФдВ,МД
ЮЊдВаФЕФдВ,МД![]() ЮЛгкдВЩЯ,дВаФЮЊ
ЮЛгкдВЩЯ,дВаФЮЊ![]() ,АыОЖЮЊ1
,АыОЖЮЊ1
Ыљвд![]() гы
гы![]() жЎМфТњзуЕФЙиЯЕЮЊ
жЎМфТњзуЕФЙиЯЕЮЊ![]()
ЃЈ2ЃЉжїЪгЭМЗжБ№ЮЊ![]() дк
дк![]() ЦНУцЩЯЕФЭЖгА,ЫљвджїЪгЭМШчЯТЫљЪО:
ЦНУцЩЯЕФЭЖгА,ЫљвджїЪгЭМШчЯТЫљЪО:

зѓЪгЭМШчЯТЭМЫљЪО:

ИУВПЗжЕФУцЛ§ЮЊ![]()
ЃЈ3ЃЉНЋдВжљВЙГфЭъећ,ВЂзїСНИіФкЧаЧђ,ЗжБ№ЧаНиУцгк![]() .Й§Еу
.Й§Еу![]() зї
зї![]() гыСНИіФкЧаЧђЗжБ№НЛгк
гыСНИіФкЧаЧђЗжБ№НЛгк![]()

гЩЧаЯпГЄЖЈРэПЩжЊ,![]()
Ыљвд![]()
гЩгк![]() ЮЊЖЈжЕ,ЫљвдгЩЭждВЖЈвхПЩжЊ,ЖЏЕу
ЮЊЖЈжЕ,ЫљвдгЩЭждВЖЈвхПЩжЊ,ЖЏЕу![]() ЕФЙьМЃЮЊЭждВ,МДНиУцЕФБпНчЪЧЭждВ
ЕФЙьМЃЮЊЭждВ,МДНиУцЕФБпНчЪЧЭждВ
![]() ,
,![]()
ЫљвдНиУцУцЛ§ЮЊ![]()



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌе§ЗНЬхABCDЉAЁфBЁфCЁфDЁфЕФРтГЄЮЊ1ЃЌEЃЌFЗжБ№ЪЧРтAAЁфЃЌCCЁфЕФжаЕуЃЌЙ§жБЯпEЃЌFЕФЦНУцЗжБ№гыРтBBЁфЁЂDDЁфНЛгкMЃЌNЃЌЩшBMЃНxЃЌxЁЪ[0ЃЌ1]ЃЌИјГівдЯТЫФИіУќЬтЃК
ЂйЦНУцMENFЁЭЦНУцBDDЁфBЁфЃЛ
ЂкЕБЧвНіЕБxЃН![]() ЪБЃЌЫФБпаЮMENFЕФУцЛ§зюаЁЃЛ
ЪБЃЌЫФБпаЮMENFЕФУцЛ§зюаЁЃЛ
ЂлЫФБпаЮMENFжмГЄLЃНfЃЈxЃЉЃЌxЁЪ[0ЃЌ1]ЪЧЕЅЕїКЏЪ§ЃЛ
ЂмЫФРтзЖCЁфЉMENFЕФЬхЛ§VЃНhЃЈxЃЉЮЊГЃКЏЪ§ЃЛ
вдЩЯУќЬтжаМйУќЬтЕФађКХЮЊЃЈЁЁЁЁЃЉ
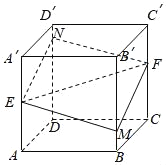
A. ЂйЂмB. ЂкC. ЂлD. ЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЧњЯп
жаЃЌЧњЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ![]() ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕуЮЊМЋЕуЃЌ
ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕуЮЊМЋЕуЃЌ ![]() жсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп
жсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп![]() ЕФМЋзјБъЮЊ
ЕФМЋзјБъЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЧњЯп![]() ЕФЦеЭЈЗНГЬКЭЧњЯп
ЕФЦеЭЈЗНГЬКЭЧњЯп![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉШєЧњЯп![]() КЭЧњЯп
КЭЧњЯп![]() гаШ§ИіЙЋЙВЕуЃЌЧѓвдетШ§ИіЙЋЙВЕуЮЊЖЅЕуЕФШ§НЧаЮЕФУцЛ§ЃЎ
гаШ§ИіЙЋЙВЕуЃЌЧѓвдетШ§ИіЙЋЙВЕуЮЊЖЅЕуЕФШ§НЧаЮЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈЂёЃЉЕБ![]() ЪБЃЌЧѓКЏЪ§
ЪБЃЌЧѓКЏЪ§![]() ЕФЕЅЕїЧјМфЃЛ
ЕФЕЅЕїЧјМфЃЛ
ЃЈЂђЃЉШєдкЧјМф![]() ЩЯДцдкВЛЯрЕШЕФЪЕЪ§
ЩЯДцдкВЛЯрЕШЕФЪЕЪ§![]() ,ЪЙ
,ЪЙ![]() ГЩСЂЃЌЧѓ
ГЩСЂЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈЂѓЃЉШєКЏЪ§![]() гаСНИіВЛЭЌЕФМЋжЕЕу
гаСНИіВЛЭЌЕФМЋжЕЕу![]() ЃЌ
ЃЌ![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПУПФъСљЁЂЦпдТЗнЃЌЮвЙњГЄНжаЯТгЮЕиЧјНјШыГжај25ЬьзѓгвЕФУЗгъМОНкЃЌШчЭМЪЧНФЯФГЕиЧј![]() Фъ10ФъМфУЗгъМОНкЕФНЕгъСП
Фъ10ФъМфУЗгъМОНкЕФНЕгъСП![]() ЕЅЮЛЃК
ЕЅЮЛЃК![]() ЕФЦЕТЪЗжВМжБЗНЭМЃЌЪдгУбљБОЦЕТЪЙРМЦзмЬхИХТЪЃЌНтД№ЯТСаЮЪЬтЃК
ЕФЦЕТЪЗжВМжБЗНЭМЃЌЪдгУбљБОЦЕТЪЙРМЦзмЬхИХТЪЃЌНтД№ЯТСаЮЪЬтЃК
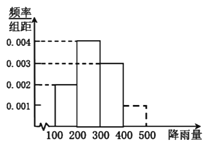
![]() МйЩшУПФъЕФУЗгъМОНкЬьЦјЯрЛЅЖРСЂЃЌЧѓИУЕиЧјЮДРДШ§ФъРяжСЩйгаСНФъУЗгъМОНкЕФНЕгъСПГЌЙ§350mmЕФИХТЪЃЎ
МйЩшУПФъЕФУЗгъМОНкЬьЦјЯрЛЅЖРСЂЃЌЧѓИУЕиЧјЮДРДШ§ФъРяжСЩйгаСНФъУЗгъМОНкЕФНЕгъСПГЌЙ§350mmЕФИХТЪЃЎ
![]() РЯРюдкИУЕиЧјГаАќСЫ20ФЖЭСЕижжжВбюУЗЃЌЫћЙ§ШЅжжжВЕФМзЦЗжжбюУЗЃЌЦНОљУПФъЕФзмРћШѓЮЊ28ЭђдЊ
РЯРюдкИУЕиЧјГаАќСЫ20ФЖЭСЕижжжВбюУЗЃЌЫћЙ§ШЅжжжВЕФМзЦЗжжбюУЗЃЌЦНОљУПФъЕФзмРћШѓЮЊ28ЭђдЊ![]() ЖјввЦЗжжбюУЗЕФФЖВњСП
ЖјввЦЗжжбюУЗЕФФЖВњСП![]() ФЖ
ФЖ![]() гыНЕгъСПжЎМфЕФЙиЯЕШчЯТУцЭГМЦБэЫљЪОЃЌгжжЊввЦЗжжбюУЗЕФЕЅЮЛРћШѓЮЊ
гыНЕгъСПжЎМфЕФЙиЯЕШчЯТУцЭГМЦБэЫљЪОЃЌгжжЊввЦЗжжбюУЗЕФЕЅЮЛРћШѓЮЊ![]() дЊ
дЊ![]() ЃЌЧыФуАяжњРЯРюЗжЮіЃЌЫћРДФъгІИУжжжВФФИіЦЗжжЕФбюУЗПЩвдЪЙзмРћШѓ
ЃЌЧыФуАяжњРЯРюЗжЮіЃЌЫћРДФъгІИУжжжВФФИіЦЗжжЕФбюУЗПЩвдЪЙзмРћШѓ![]() ЭђдЊ
ЭђдЊ![]() ЕФЦкЭћИќДѓЃПВЂЫЕУїРэгЩЃЎ
ЕФЦкЭћИќДѓЃПВЂЫЕУїРэгЩЃЎ
НЕгъСП |
|
|
|
|
ФЖВњСП | 500 | 700 | 600 | 400 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋдАзМБИдквЛдВаЮЫЎГиРяЩшжУСНИіЙлОАХчШЊЃЌЙлОАХчШЊЕФЪОвтЭМШчЭМЫљЪОЃЌ![]() СНЕуЮЊХчШЊЃЌдВаФ
СНЕуЮЊХчШЊЃЌдВаФ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌЦфжа
ЕФжаЕуЃЌЦфжа![]() УзЃЌАыОЖ
УзЃЌАыОЖ![]() УзЃЌЪаУёПЩЮЛгкЫЎГиБпдЕШЮвтвЛЕу
УзЃЌЪаУёПЩЮЛгкЫЎГиБпдЕШЮвтвЛЕу![]() ДІЙлЩЭЃЎ
ДІЙлЩЭЃЎ
ЃЈ1ЃЉШєЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌЧѓДЫЪБ
ЃЌЧѓДЫЪБ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЩш![]() ЃЌЧв
ЃЌЧв![]() ЃЎ
ЃЎ
ЃЈiЃЉЪдНЋ![]() БэЪОЮЊ
БэЪОЮЊ![]() ЕФКЏЪ§ЃЌВЂЧѓГі
ЕФКЏЪ§ЃЌВЂЧѓГі![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈiiЃЉШєЭЌЪБвЊЧѓЪаУёдкЫЎГиБпдЕШЮвтвЛЕу![]() ДІЙлЩЭХчШЊЪБЃЌЙлЩЭНЧЖШ
ДІЙлЩЭХчШЊЪБЃЌЙлЩЭНЧЖШ![]() ЕФзюДѓжЕВЛаЁгк
ЕФзюДѓжЕВЛаЁгк![]() ЃЌЪдЧѓ
ЃЌЪдЧѓ![]() СНДІХчШЊМфОрРыЕФзюаЁжЕЃЎ
СНДІХчШЊМфОрРыЕФзюаЁжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЪ§Са ![]() жаЃЌвбжЊ
жаЃЌвбжЊ ![]() ЃЌ
ЃЌ![]() ЮЊГЃЪ§.
ЮЊГЃЪ§.
(1)жЄУї: ![]() ГЩЕШВюЪ§Са;
ГЩЕШВюЪ§Са;
(2)Щш ![]() ЃЌЧѓЪ§Са
ЃЌЧѓЪ§Са![]() ЕФЧАnЯюКЭ
ЕФЧАnЯюКЭ ![]() ЃЛ
ЃЛ
(3)ЕБ![]() ЪБЃЌЪ§Са
ЪБЃЌЪ§Са ![]() жаЪЧЗёДцдкВЛЭЌЕФШ§Яю
жаЪЧЗёДцдкВЛЭЌЕФШ§Яю![]() ГЩЕШБШЪ§СаЃЌ
ГЩЕШБШЪ§СаЃЌ
Чв![]() вВГЩЕШБШЪ§Са?ШєДцдкЃЌЧѓГі
вВГЩЕШБШЪ§Са?ШєДцдкЃЌЧѓГі![]() ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжьЪРНмЪЧРњЪЗЩЯзюЮАДѓЕФЪ§бЇМвжЎвЛЃЌЫћЫљжјЕФЁЖЫФдЊгёМјЁЗОэжаЁАШчЯёеаЪ§ЁБЮхЮЪжагаШчЯТЮЪЬтЃКНёгаЙйЫОВюЗђвЛЧЇАЫАйСљЪЎЫФШЫжўЕЬЃЌжЛдЦГѕШеВюСљЪЎЫФШЫЃЌДЮШезЊЖрЦпШЫ.ЁБЦфДѓвтЮЊЁАЙйИЎТНајХЩЧВ1864ШЫЧАЭљаожўЕЬАгЃЌЕквЛЬьХЩГі64ШЫЃЌДгЕкЖўЬьПЊЪМУПЬьХЩГіЕФШЫЪ§БШЧАвЛЬьЖр7ШЫ.ЁБдкИУЮЪЬтжаЕФ1864ШЫШЋВПХЩЧВЕНЮЛашвЊЕФЬьЪ§ЮЊЃЈ ЃЉ
A. 9B. 16C. 18D. 20
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжабЇ2018ФъЕФИпПМПМЩњШЫЪ§ЪЧ2015ФъИпПМПМЩњШЫЪ§ЕФ![]() БЖЃЌЮЊСЫИќКУЕиЖдБШИУаЃПМЩњЕФЩ§бЇЧщПіЃЌЭГМЦСЫИУаЃ2015ФъКЭ2018ФъЕФИпПМЧщПіЃЌЕУЕНШчЭМжљзДЭМЃК
БЖЃЌЮЊСЫИќКУЕиЖдБШИУаЃПМЩњЕФЩ§бЇЧщПіЃЌЭГМЦСЫИУаЃ2015ФъКЭ2018ФъЕФИпПМЧщПіЃЌЕУЕНШчЭМжљзДЭМЃК

дђЯТСаНсТле§ШЗЕФЪЧ![]() ЁЁЁЁ
ЁЁЁЁ![]()
A. гы2015ФъЯрБШЃЌ2018ФъвЛБОДяЯпШЫЪ§МѕЩй
B. гы2015ФъЯрБШЃЌ2018ФъЖўБОДяЯпШЫЪ§діМгСЫ![]() БЖ
БЖ
C. 2015Фъгы2018ФъвеЬхДяЯпШЫЪ§ЯрЭЌ
D. гы2015ФъЯрБШЃЌ2018ФъВЛЩЯЯпЕФШЫЪ§гаЫљдіМг
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com