
分析 抛物线y2=4$\sqrt{3}$x的焦点为F($\sqrt{3}$,0),其准线方程为x=-$\sqrt{3}$,利用△FAB为正三角形,可得A的坐标,代入双曲线的方程,可得a,b的方程,利用双曲线的一条渐近线方程是y=$\sqrt{2}$x,可得a,b的方程,从而可得a,b的值,即可求出双曲线的方程.
解答 解:抛物线y2=4$\sqrt{3}$x的焦点为F($\sqrt{3}$,0),其准线方程为x=-$\sqrt{3}$,
∵△FAB为正三角形,
∴|AB|=4,
将(-$\sqrt{3}$,2)代入双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1可得$\frac{3}{{a}^{2}}-\frac{4}{{b}^{2}}$=1,
∵双曲线的一条渐近线方程是y=$\sqrt{2}$x,∴$\frac{b}{a}$=$\sqrt{2}$,
∴a=1,b=$\sqrt{2}$,
∴双曲线C2的方程为${x^2}-\frac{y^2}{2}=1$.
故答案为${x^2}-\frac{y^2}{2}=1$.
点评 本题考查抛物线、双曲线的方程与性质,考查学生的计算能力,正确运用抛物线、双曲线的性质是关键.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
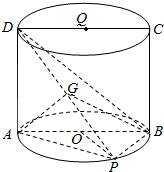 如图,四边形ABCD是体积为8$\sqrt{3}$π的圆柱OQ的轴截面,点P在底面圆周上,BP=OA=2,G是DP的中点.
如图,四边形ABCD是体积为8$\sqrt{3}$π的圆柱OQ的轴截面,点P在底面圆周上,BP=OA=2,G是DP的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 143 | B. | 144 | C. | 287 | D. | 288 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+2y-3=0 | B. | 2x-y+4=0 | C. | x+2y+3=0 | D. | x+2y-5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 锐角三角形 | ||
| C. | 钝角三角形 | D. | 以上情况都有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,3] | B. | [-1,2] | C. | [-3,2] | D. | (-1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com