
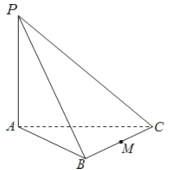
【题目】如图,三棱锥![]() 中,
中,![]() 底面ABC,M是 BC的中点,若底面ABC是边长为2的正三角形,且PB与底面ABC所成的角为
底面ABC,M是 BC的中点,若底面ABC是边长为2的正三角形,且PB与底面ABC所成的角为![]() . 求:
. 求:
(1)三棱锥![]() 的体积;
的体积;
(2)异面直线PM与AC所成角的大小. (结果用反三角函数值表示)
【答案】(1)2;(2)![]() .
.
【解析】
试题(1)欲求三棱锥P-ABC的体积,只需求出底面积和高即可,因为底面ABC是边长为2的正三角形,所以底面积可用![]() 来计算,其中a是正三角形的边长,又因为PA⊥底面ABC,所以三棱锥的高就是PA长,再代入三棱锥的体积公式即可.(2)欲求异面直线所成角,只需平移两条异面直线中的一条,是它们成为相交直线即可,由M为BC中点,可借助三角形的中位线平行于第三边的性质,做出
来计算,其中a是正三角形的边长,又因为PA⊥底面ABC,所以三棱锥的高就是PA长,再代入三棱锥的体积公式即可.(2)欲求异面直线所成角,只需平移两条异面直线中的一条,是它们成为相交直线即可,由M为BC中点,可借助三角形的中位线平行于第三边的性质,做出![]() 的中位线,就可平移BC,把异面直线所成角转化为平面角,再放入
的中位线,就可平移BC,把异面直线所成角转化为平面角,再放入![]() 中,求出角即可.
中,求出角即可.
试题解析:(1)因为![]() 底面
底面![]() ,
,![]() 与底面
与底面![]() 所成的角为
所成的角为![]()
所以![]() , 因为
, 因为![]() ,所以
,所以![]()
![]()
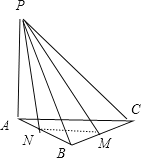
(2)连接![]() ,取
,取![]() 的中点,记为
的中点,记为![]() ,连接
,连接![]() ,则
,则![]()
所以![]() 为异面直线
为异面直线![]() 与
与![]() 所成的角
所成的角
计算可得:![]() ,
,![]() ,
,![]()
![]()
异面直线![]() 与
与![]() 所成的角为
所成的角为![]() .
.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
【题目】在某次水下考古活动中,需要潜水员潜入水深为30米的水底进行作业.其用氧量包含3个方面:①下潜时,平均速度为![]() (米/单位时间),单位时间内用氧量为
(米/单位时间),单位时间内用氧量为![]() (
(![]() 为正常数);②在水底作业需5个单位时间,每个单位时间用氧量为0.4;③返回水面时,平均速度为
为正常数);②在水底作业需5个单位时间,每个单位时间用氧量为0.4;③返回水面时,平均速度为![]() (米/单位时间), 单位时间用氧量为0.2.记该潜水员在此次考古活动中,总用氧量为
(米/单位时间), 单位时间用氧量为0.2.记该潜水员在此次考古活动中,总用氧量为![]() .
.
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)设0<![]() ≤5,试确定下潜速度
≤5,试确定下潜速度![]() ,使总的用氧量最少.
,使总的用氧量最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图是一几何体的平面展开图,其中四边形ABCD为正方形,E,F,G,H分别为![]() ,
,![]() ,
,![]() ,
,![]() 的中点,在此几何体中,给出下面五个结论:①平面
的中点,在此几何体中,给出下面五个结论:①平面![]() 平面ABCD;②
平面ABCD;②![]() 平面BDG;③
平面BDG;③![]() 平面PBC;④
平面PBC;④![]() 平面BDG;⑤
平面BDG;⑤![]() 平面BDG.
平面BDG.
其中正确结论的序号是________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 为定义域
为定义域![]() 上单调函数,且存在区间
上单调函数,且存在区间![]() (其中
(其中![]() ),使得当
),使得当![]() 时,
时,![]() 的值域恰为
的值域恰为![]() ,则称函数
,则称函数![]() 是
是![]() 上的正函数,区间
上的正函数,区间![]() 叫做等域区间.如果函数
叫做等域区间.如果函数![]() 是
是![]() 上的正函数,则实数
上的正函数,则实数![]() 的取值范围为 ▲ .
的取值范围为 ▲ .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆![]() :
:![]() .
.

(Ⅰ)若圆C与x轴相切,求圆C的方程;
(Ⅱ)已知![]() ,圆
,圆![]() 与x轴相交于两点
与x轴相交于两点![]() (点
(点![]() 在点
在点![]() 的左侧).过点
的左侧).过点![]() 任作一条直线与圆
任作一条直线与圆![]() :
:![]() 相交于两点A,B.问:是否存在实数a,使得
相交于两点A,B.问:是否存在实数a,使得![]() =
=![]() ?若存在,求出实数a的值,若不存在,请说明理由.
?若存在,求出实数a的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com