
【题目】若将函数f(x)=cosx(sinx+cosx)﹣ ![]() 的图象向右平移φ个单位,所得函数是奇函数,则φ的最小正值是( )
的图象向右平移φ个单位,所得函数是奇函数,则φ的最小正值是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:将函数f(x)=cosx(sinx+cosx)﹣ ![]() =
= ![]() sin2x+
sin2x+ ![]() ﹣
﹣ ![]() =
= ![]() sin(2x+
sin(2x+ ![]() ) 的图象向右平移φ个单位,
) 的图象向右平移φ个单位,
得到y= ![]() sin[2(x﹣φ)+
sin[2(x﹣φ)+ ![]() ]=
]= ![]() sin(2x+
sin(2x+ ![]() ﹣2φ)的图象.
﹣2φ)的图象.
再根据所得函数是奇函数,则 ![]() ﹣2φ=kπ,k∈Z,则φ的最小正值为
﹣2φ=kπ,k∈Z,则φ的最小正值为 ![]() ,
,
故选:D.
【考点精析】掌握函数y=Asin(ωx+φ)的图象变换是解答本题的根本,需要知道图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


科目:高中数学 来源: 题型:
【题目】某班同学利用寒假进行社会实践活动,对![]() 岁的人群随机抽取
岁的人群随机抽取![]() 人进行了一次生活习惯是
人进行了一次生活习惯是
否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得
到如下统计表和各年龄段人数频率分布直方图:
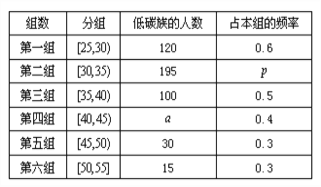
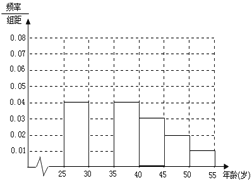
(I)补全频率分布直方图并求![]() 、
、![]() 、
、![]() 的值;
的值;
(II)从年龄段在![]() 的“低碳族”中采用分层抽样法抽取
的“低碳族”中采用分层抽样法抽取![]() 人参加户外低碳体验活动,其中选取
人参加户外低碳体验活动,其中选取![]() 人作为领队,求选取的
人作为领队,求选取的![]() 名领队中恰有1人年龄在
名领队中恰有1人年龄在![]() 岁的概率.
岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD-A1B1C1D中,S是B1D1的中点,E、F、G分别是BC、CD和SC的中点.求证:
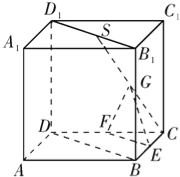
(1)直线EG∥平面BDD1B1;
(2)平面EFG∥平面BDD1B1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区交管部门为了对该地区驾驶员的某项考试成绩进行分析,随机抽取了15分到45分之间的1000名学员的成绩,并根据这1000名驾驶员的成绩画出样本的频率分布直方图(如图),则成绩在[30,35)内的驾驶员人数共有( ) 
A.60
B.180
C.300
D.360
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 为正方体,给出以下五个结论:
为正方体,给出以下五个结论:
① ![]() 平面
平面![]() ;
;
② ![]() ⊥平面
⊥平面![]() ;
;
③ ![]() 与底面
与底面![]() 所成角的正切值是
所成角的正切值是![]() ;
;
④ 二面角![]() 的正切值是
的正切值是![]() ;
;
⑤ 过点![]() 且与异面直线
且与异面直线![]() 和
和 ![]() 均成70°角的直线有4条.
均成70°角的直线有4条.
其中,所有正确结论的序号为________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的参数方程为: ![]() (φ为参数),直线l的极坐标方程为ρ(cosθ+sinθ)=4.
(φ为参数),直线l的极坐标方程为ρ(cosθ+sinθ)=4.
(1)求曲线C的普通方程和直线l的直角坐标方程;
(2)若点P在曲线C上,点Q在直线l上,求线段PQ的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com