考点:命题的真假判断与应用
专题:计算题,数形结合,函数的性质及应用,不等式的解法及应用
分析:画出函数f(x)=
(a是常数且a>0)的图象,
①由图只需说明在点x=0处函数f(x)的最小值是-1;
②只需说明函数f(x)在R上的单调性即可;
③函数f(x)在(-∞,0)的零点是lg
;
④只需说明f(x)>0在[
,+∞)上恒成立,则当x=
时,函数取得最小值,
从而求得a的取值范围是a>1;
⑤已知函数f(x)的图象在(-∞,0))上是下凹的,所以任取两点连线应在图象的上方.
解答:
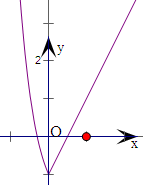
解:对于①,由图只需说明在点x=0处函数f(x)的最小值是-1;故正确;
对于②,由图象说明函函数f(x)在R上不是单调函数;故错;
对于③,函数f(x)在(-∞,0)的零点是lg
,故正确;
对于④,只需说明f(x)>0在[
,+∞)上恒成立,则当x=
时,函数取得最小值,求得a的取值范围是a>1;故错;
对于⑤,已知函数f(x)在(-∞,0)上的图象是下凹的,所以任取两点连线应在图象的上方,即f(
)<
,故正确.
故答案为:①③⑤.
点评:利用函数的图象研究函数的单调区间,以及根据函数的增减性得到函数的最值是常用的方法,解答本题的关键是图象法.

 解:对于①,由图只需说明在点x=0处函数f(x)的最小值是-1;故正确;
解:对于①,由图只需说明在点x=0处函数f(x)的最小值是-1;故正确;

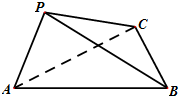 如图,在三棱锥P-ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,平面PAB⊥平面ABC.
如图,在三棱锥P-ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,平面PAB⊥平面ABC.