
【题目】已知![]() 表示两个不同的平面,
表示两个不同的平面, ![]() 表示两条不同直线,对于下列两个命题:
表示两条不同直线,对于下列两个命题:
①若![]() ,则“
,则“![]() ”是“
”是“![]() ”的充分不必要条件;
”的充分不必要条件;
②若![]() ,则“
,则“![]() ”是“
”是“![]() 且
且![]() ”的充要条件.判读正确的是( )
”的充要条件.判读正确的是( )
A. ①②都是真命题 B. ①是真命题,②是假命题
C. ①是假命题,②是真命题 D. ①②都是假命题
科目:高中数学 来源: 题型:
【题目】水葫芦原产于巴西,![]() 年作为观赏植物引入中国. 现在南方一些水域水葫芦已泛滥成灾严重影响航道安全和水生动物生长. 某科研团队在某水域放入一定量水葫芦进行研究,发现其蔓延速度越来越快,经过
年作为观赏植物引入中国. 现在南方一些水域水葫芦已泛滥成灾严重影响航道安全和水生动物生长. 某科研团队在某水域放入一定量水葫芦进行研究,发现其蔓延速度越来越快,经过![]() 个月其覆盖面积为
个月其覆盖面积为![]() ,经过
,经过![]() 个月其覆盖面积为
个月其覆盖面积为![]() . 现水葫芦覆盖面积
. 现水葫芦覆盖面积![]() (单位
(单位![]() )与经过时间
)与经过时间![]() 个月的关系有两个函数模型
个月的关系有两个函数模型![]() 与
与![]() 可供选择.
可供选择.
(参考数据:![]() )
)
(Ⅰ)试判断哪个函数模型更合适,并求出该模型的解析式;
(Ⅱ)求原先投放的水葫芦的面积并求约经过几个月该水域中水葫芦面积是当初投放的![]() 倍.
倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“双曲线的方程为![]() ”是“双曲线的渐近线方程为
”是“双曲线的渐近线方程为![]() ”的( )
”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
【答案】A
【解析】双曲线的方程为![]() ,则渐近线方程为
,则渐近线方程为![]() ,渐近线方程为:
,渐近线方程为: ![]() ,反之当渐近线方程为
,反之当渐近线方程为![]() 时,只需要满足
时,只需要满足![]() ,等轴双曲线即可.故选择充分不必要条件.
,等轴双曲线即可.故选择充分不必要条件.
故答案为:A.
【题型】单选题
【结束】
10
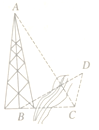
【题目】如图,为测量河对岸塔![]() 的高,先在河岸上选一点
的高,先在河岸上选一点![]() ,使
,使![]() 在塔底
在塔底![]() 的正东方向上,在点
的正东方向上,在点![]() 处测得
处测得![]() 点的仰角为
点的仰角为![]() ,再由点
,再由点![]() 沿北偏东
沿北偏东![]() 方向走
方向走![]() 到位置
到位置![]() ,测得
,测得![]() ,则塔
,则塔![]() 的高是( )
的高是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)根据二倍角公式和两角和差公式得到![]() ,进而得到周期;(2)由
,进而得到周期;(2)由![]() ,得到
,得到![]() ,
, ![]() ,由配凑角公式得到
,由配凑角公式得到![]() ,代入值得到函数值.
,代入值得到函数值.
解析:
(1)由题意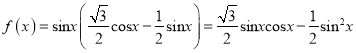
![]() =
=![]()
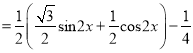
![]()
所以![]() 的最小正周期为
的最小正周期为![]() ;
;
(2)由![]()
![]()
又由![]() 得
得![]() ,所以
,所以![]()
故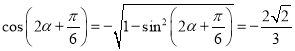 ,
,
故![]()
![]()
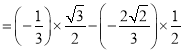
![]()
【题型】解答题
【结束】
20
【题目】为响应十九大报告提出的实施乡村振兴战略,某村庄投资![]() 万元建起了一座绿色农产品加工厂.经营中,第一年支出
万元建起了一座绿色农产品加工厂.经营中,第一年支出![]() 万元,以后每年的支出比上一年增加了
万元,以后每年的支出比上一年增加了![]() 万元,从第一年起每年农场品销售收入为
万元,从第一年起每年农场品销售收入为![]() 万元(前
万元(前![]() 年的纯利润综合=前
年的纯利润综合=前![]() 年的 总收入-前
年的 总收入-前![]() 年的总支出-投资额
年的总支出-投资额![]() 万元).
万元).
(1)该厂从第几年开始盈利?
(2)该厂第几年年平均纯利润达到最大?并求出年平均纯利润的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 为正方形,四边形
为正方形,四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() .
.
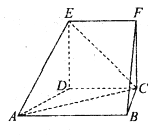
(1)求![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)线段![]() 或其延长线上是否存在点
或其延长线上是否存在点![]() ,使平面
,使平面![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的方程为![]() ,过点
,过点![]() 的直线
的直线![]() 与抛物线相交于
与抛物线相交于![]() 两点,分别过点
两点,分别过点![]() 作抛物线的两条切线
作抛物线的两条切线![]() 和
和![]() ,记
,记![]() 和
和![]() 相交于点
相交于点![]() .
.
(1)证明:直线![]() 和
和![]() 的斜率之积为定值;
的斜率之积为定值;
(2)求证:点![]() 在一条定直线上.
在一条定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线W:y2=4x与圆C:(x-1)2+y2=25交于A,B两点,点P为劣弧![]() 上不同于A,B的一个动点,与x轴平行的直线PQ交抛物线W于点Q,则△PQC的周长的取值范围是( )
上不同于A,B的一个动点,与x轴平行的直线PQ交抛物线W于点Q,则△PQC的周长的取值范围是( )
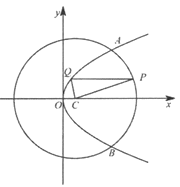
A. (10,14) B. (12,14)
C. (10,12) D. (9,11)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义在
是定义在![]() 上的偶函数,且对任意的
上的偶函数,且对任意的![]() 恒有
恒有![]() ,已知当
,已知当![]() 时,
时,![]() ,则下列命题:
,则下列命题:
①对任意![]() ,都有
,都有![]() ;②函数
;②函数![]() 在
在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
③函数![]() 的最大值是1,最小值是0;④当
的最大值是1,最小值是0;④当![]() 时,
时,![]() .
.
其中正确命题的序号有________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com