
【题目】下列命题中正确的是( )
A.若p∨q为真命题,则p∧q为真命题
B.“a>0,b>0”是“ ![]() ≥2”的充分必要条件
≥2”的充分必要条件
C.命题“若x2﹣3x+2=0,则x=1或x=2”的逆否命题为“若x≠1或x≠2,则x2﹣3x+2≠0”
D.命题p:?x∈R,使得x2+x﹣1<0,则¬p:?x∈R,使得x2+x﹣1≥0
【答案】D
【解析】解:对于A.若p∨q为真命题,则p,q中至少有一个为真,则p∧q的真假不定,则A错误;
对于B.若a>0,b>0,则 ![]() ≥2
≥2 ![]() =2,当且仅当a=b取得等号,反之,若
=2,当且仅当a=b取得等号,反之,若 ![]() ≥2即为
≥2即为 ![]() ≥0,即
≥0,即 ![]() ≥0,即有ab>0,则“a>0,b>0”是“
≥0,即有ab>0,则“a>0,b>0”是“ ![]() ≥2”的充分不必要条件,则B错误;
≥2”的充分不必要条件,则B错误;
对于C.命题“若x2﹣3x+2=0,则x=1或x=2”的逆否命题为“若x≠1且x≠2,则x2﹣3x+2≠0”,则C错误;
对于D.命题p:x∈R,使得x2+x﹣1<0,则¬p:x∈R,使得x2+x﹣1≥0,则D正确.
故选D.
【考点精析】认真审题,首先需要了解命题的真假判断与应用(两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系).


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】设集合P={m|﹣1<m≤0},Q={m|mx2+4mx﹣4<0对任意x恒成立},则P与Q的关系是( )
A.PQ
B.QP
C.P=Q
D.P∩Q=
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直,AA1=AB=AC=2,BC=2 ![]() ,M,N分别是CC1 , BC的中点,点P在直线A1B1上,且
,M,N分别是CC1 , BC的中点,点P在直线A1B1上,且 ![]() .
. 
(1)证明:无论λ取何值,总有AM⊥PN;
(2)当λ取何值时,直线PN与平面ABC所成的角θ最大?并求该角取最大值时的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在多面体ABCDE中,BC=BA,DE∥BC,AE⊥平面BCDE,BC=2DE,F为AB的中点. 
(1)求证:EF∥平面ACD;
(2)若EA=EB=CD,求二面角B﹣AD﹣E的正切值的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,当x∈[0,+∞)时,f(x)=2x﹣2,则不等式f(log2x)>0的解集为( )
A.(0, ![]() )
)
B.( ![]() ,1)∪(2,+∞)
,1)∪(2,+∞)
C.(2,+∞)
D.(0, ![]() )∪(2,+∞)
)∪(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆C1: ![]() +y2=1,x轴被曲线C2:y=x2﹣b截得的线段长等于C1的长半轴长.
+y2=1,x轴被曲线C2:y=x2﹣b截得的线段长等于C1的长半轴长. 
(1)求实数b的值;
(2)设C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A、B,直线MA、MB分别与C1相交于D、E.
①证明: ![]() =0;
=0;
②记△MAB,△MDE的面积分别是S1 , S2 . 若 ![]() =λ,求λ的取值范围.
=λ,求λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(ax2﹣x+1),其中a>0且a≠1.
(1)当a= ![]() 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(2)当f(x)在区间 ![]() 上为增函数时,求实数a的取值范围.
上为增函数时,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1中,侧棱AA1⊥平面ABC.若AB=AC=AA1=1,BC= ![]() ,则异面直线A1C与B1C1所成的角为 . .
,则异面直线A1C与B1C1所成的角为 . . 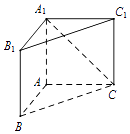
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com