
 如图:Rt△ABC中,∠CAB=90°,AB=2,AC=$\frac{\sqrt{2}}{2}$,曲线E过C点,动点P在E上运动,且保持|PA|+|PB|的值不变.
如图:Rt△ABC中,∠CAB=90°,AB=2,AC=$\frac{\sqrt{2}}{2}$,曲线E过C点,动点P在E上运动,且保持|PA|+|PB|的值不变.分析 (1)由题意可知:|PA|+|PB|=|CA|+|CB|=2$\sqrt{2}$,动点的轨迹是以为A,B焦点椭圆,即2a=2$\sqrt{2}$,a=$\sqrt{2}$,2c=2,b2=a2-c2=1,即可求得椭圆的方程;
(2)直线l得方程为y=-$\sqrt{3}$(x-1),代入椭圆方程,利用韦达定理及弦长公式即可求得|MN|的长度.
解答 解:(1)以AB、OD所在的直线分别为x轴、y轴,O为原点建立直角坐标系….(1分)
∵|PA|+|PB|=|CA|+|CB|=$\frac{{\sqrt{2}}}{2}$+$\sqrt{{2^2}+{{(\frac{{\sqrt{2}}}{2})}^2}}$=2$\sqrt{2}$,
动点的轨迹是以为A,B焦点椭圆….(4分)
设其长、短半轴的长分别为a、b,半焦距为c,则a=$\sqrt{2}$,c=1,b=1,
∴曲线E的方程为:$\frac{x^2}{2}$+y2=1.…(6分)
(2)直线l得方程为y=-$\sqrt{3}$(x-1)且M(x1,y1),N(x2,y2)….(7分)
由方程组$\left\{\begin{array}{l}y=-\sqrt{3}(x-1)\\ \frac{x^2}{2}+{y^2}=1\end{array}\right.$,得方程7x2-12x+4=0
x1+x2=$\frac{12}{7}$,x1•x2=$\frac{4}{7}$ …(9分)
$|MN|=\sqrt{1+{{(-\sqrt{3})}^2}}|{x_1}-{x_2}|$=$2\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}$=$2\sqrt{{{(\frac{12}{7})}^2}-4×\frac{4}{7}}=\frac{{8\sqrt{2}}}{7}$,
故$|{MN}|=\frac{{8\sqrt{2}}}{7}$…..(12分)
点评 本题考查椭圆的定义及标准方程,考查直线与椭圆的位置关系,韦达定理及弦长公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $(-3,-\frac{5}{2})$ | B. | $(2,\frac{5}{2})$ | C. | $(\frac{5}{2},3)$ | D. | $(-3,\frac{5}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
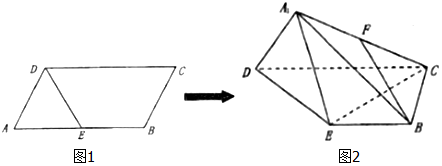
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
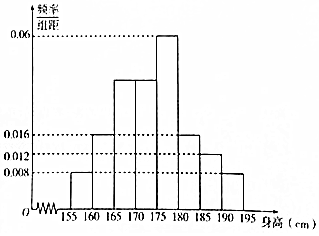 从某校高一年级1000名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米到195厘米之间,将测量结果分为八组:第一组[155,160),第二组[160,165),…,第八组[190,195),得到频率分布直方图如图所示.
从某校高一年级1000名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米到195厘米之间,将测量结果分为八组:第一组[155,160),第二组[160,165),…,第八组[190,195),得到频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若α⊥β,α⊥γ,则β⊥γ | B. | 若a,b与c所成的角相等,则a∥b | ||
| C. | 若α⊥α,α∥β,则α⊥β | D. | 若a∥b,a?α,则b∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | ||
| C. | 2个 | D. | 不确定,随k的变化而变化 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com