
����Ŀ��ij�������ȡ������ҵ�������Ͻ�˰�����{��λ��Ԫ�����������ݻ��Ƴ�Ƶ�ʷֲ�ֱ��ͼ����ͼ�������Ͻ�˰�շ�Χ��[0��100]�������ݷ���Ϊ[0��20����[20��40��[40��60��[60��80����[80��100��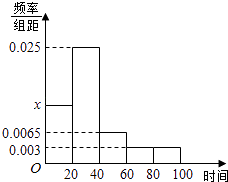
��1����ֱ��ͼ��x��ֵ��
��2��������Ͻ�˰�ղ�����60��Ԫ����ҵ�����������Żݣ�������ȡ��ҵ1200�����Թ����ж�����ҵ�������������Żݣ�
��3������ҵ����ѡ4������4����ҵ���Ͻ�˰������20��Ԫ�ĸ�����ΪX����X�ķֲ��к���ѧ��������ֱ��ͼ�е�Ƶ����Ϊ���ʣ�
���𰸡�
��1���⣺��Ƶ�ʷֲ�ֱ��ͼ�ã�
��x+0.025+0.0065+0.003+0.003����20=1��
���x=0.0125��
��2����Ƶ�ʷֲ�ֱ��ͼ�����Ͻ�˰�ղ�����60��Ԫ����ҵ��ռƵ��Ϊ��0.003+0.003����20=0.12��
�����Ͻ�˰�ղ�����60��Ԫ����ҵ�����������Żݣ�����ȡ��ҵ1200����
������У�1200��0.12=144����ҵ�������������Żݣ�
��3����ҵ���Ͻ�˰������20��Ԫ��Ƶ��p=0.0125��20=0.25��
����ҵ����ѡ4������4����ҵ���Ͻ�˰������20��Ԫ�ĸ�����ΪX��
��X��B��4�� ![]() ����
����
P��X=0��= ![]() =
= ![]() ��
��
P��X=1��= ![]() =
= ![]() ��
��
P��X=2��= ![]() =
= ![]() ��
��
P��X=3��= ![]() =
= ![]() ��
��
P��X=4��= ![]() =
= ![]() ��
��
��X�ķֲ���Ϊ��
X | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
E��X��= ![]() =1��
=1��
����������1����Ƶ��ֱ��ͼ�������Ϊ1�ɵ�x��ֵ����2����Ƶ�ʷֲ�ֱ��ͼ��������Ͻ�˰�ղ�����60��Ԫ����ҵ��ռƵ��Ϊ0.12���ɹ��Ƴ���144����ҵ���������Żݣ���3����ҵ���Ͻ�˰������20��Ԫ��Ƶ��Ϊ0.25����ѡ�ĸ���ҵ���Ͻ�˰������20��Ԫ����ȡֵΪ0��1,2,3,4��������ʣ��г��ֲ��У�������� .


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���Ե�OΪԲ�ģ��뾶Ϊ2����Բ�β�ƺ����ƺ�ھ���O�� ![]() ����D����һ���ڹ�ȵ�ˮ��ͷ����������D��һ����ֱС·����ƺԲ����A��B���㣬Ϊ�˷������ɢ����ͬʱ��С·OA��OB������С·�Ŀ��Ⱥ��Բ��ƣ�
����D����һ���ڹ�ȵ�ˮ��ͷ����������D��һ����ֱС·����ƺԲ����A��B���㣬Ϊ�˷������ɢ����ͬʱ��С·OA��OB������С·�Ŀ��Ⱥ��Բ��ƣ�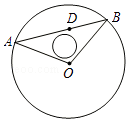
��1����Ҫʹ����С·�ķ�����ʡ������С·����̳��ȣ�
��2����Ҫ�ڡ�ABO�����ڣ����߽磩�滮��һ��Բ�εij����������������㳡�裬�������Բ�ι㳡����������������������źͦУ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�Ƽ���˾����һ���ֻ�����оƬ��������������ָ�껮��Ϊ��ָ����ڻ����70Ϊ�ϸ�Ʒ��С��70Ϊ��Ʒ���������ȡ����оƬ��120�����м�⣬�����ͳ�������
����ָ�� | [50��60�� | [60��70�� | [70��80�� | [80��90�� | [90��100] |
оƬ���������� | 8 | 22 | 45 | 37 | 8 |
��֪����һ��оƬ�����Ǻϸ�Ʒ��ӯ��400Ԫ�����Ǵ�Ʒ�����50Ԫ��
�����Թ�������һ��оƬΪ�ϸ�Ʒ�ĸ��ʣ���������3��оƬ����õ���������700Ԫ�ĸ��ʣ�
���Ǧ�Ϊ����4��оƬ���õ�����������������εķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ���ϣ���A��CΪ����PM�ϵ����㣬��B��DΪ����PN�ϵ����㣬���� ![]() ������S��PAB��S��PCD�ֱ�Ϊ��PAB����PCD����������ռ��У���A��CΪ����PM�ϵ����㣬��B��DΪ����PN�ϵ����㣬��E��FΪ����PL�ϵ����㣬����
������S��PAB��S��PCD�ֱ�Ϊ��PAB����PCD����������ռ��У���A��CΪ����PM�ϵ����㣬��B��DΪ����PN�ϵ����㣬��E��FΪ����PL�ϵ����㣬���� ![]() =������VP��ABE��VP��CDF�ֱ�Ϊ������P��ABE��P��CDF���������
=������VP��ABE��VP��CDF�ֱ�Ϊ������P��ABE��P��CDF���������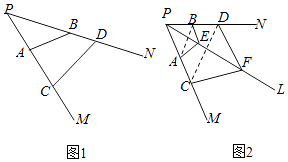
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������G��y2=2px��p��0������F��ֱ��l��������G����M��N���㣨M��x���Ϸ��������� ![]() ��
�� ![]() ������MΪԲ�����������������е�Բ�ı�����Ϊ��������
������MΪԲ�����������������е�Բ�ı�����Ϊ��������
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y= ![]() ��y=ln��1��x���Ķ�����ֱ�ΪM��N����M��N=��������
��y=ln��1��x���Ķ�����ֱ�ΪM��N����M��N=��������
A.��1��2]
B.[1��2]
C.�����ޣ�1]�ȣ�2��+�ޣ�
D.�����ޣ�1����[2��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯�� ![]() ��
��
��1����֤�� ![]() ��
��
��2����x��1ʱ��f��x����lnx��a��x��1�����������a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y2=2px��p��0����FΪ�佹�㣬���㣨4��0������ֱ��x���ֱ�߽���������A��B���㣬��ABF���ܳ�Ϊ18��
��1���������ߵķ��̣�
��2�����������ϵĶ��� ![]() ����������ֱ��y=p�ԳƵ�ֱ�߷ֱ���������C��D���㣬����CD���ж�ֱ��CD��б���Ƿ�Ϊ��ֵ����֤����Ľ��ۣ�
����������ֱ��y=p�ԳƵ�ֱ�߷ֱ���������C��D���㣬����CD���ж�ֱ��CD��б���Ƿ�Ϊ��ֵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼ�����ϵ�У�ԲC�ļ����귽��Ϊ����2=4�ѣ�cos��+sin�ȣ���6�����Լ���OΪԭ�㣬��������ֱ��Ϊx�Ὠ��ƽ��ֱ������ϵ��
������ԲC�IJ������̣�
������ֱ������ϵ�У���P��x��y����ԲC�϶��㣬����x+y�����ֵ���������ʱ��P��ֱ�����꣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com