
【题目】如图所示,已知抛物线C1:x2=2py的焦点在抛物线C2:![]() ,点P是抛物线C1上的动点.
,点P是抛物线C1上的动点.

(1)求抛物线C1的方程及其准线方程;
(2)过点P作抛物线C2的两条切线,M,N分别为两个切点,设点P到直线MN的距离为d,求d的最小值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)由题意抛物线C1的焦点为抛物线C2的顶点(0,1),由此算出p=2,从而得到抛物线C1的方程,得到C1的准线方程;(2)设P(2t,t2),用直线方程的点斜式列出直线PM方程并将点P坐标代入,化简可得![]() 同理得到
同理得到![]() .然后利用一元二次方程根与系数的关系,算出x1+x2=4t,x1x2=2t2﹣2,将直线MN的两点式方程化简并代入前面算出的式可得MN的方程为y=2tx+2﹣t2.最后利用点到直线的距离公式列式,采用换元法并且运用基本不等式求最值,即可算出P到直线MN的距离d的最小值为
.然后利用一元二次方程根与系数的关系,算出x1+x2=4t,x1x2=2t2﹣2,将直线MN的两点式方程化简并代入前面算出的式可得MN的方程为y=2tx+2﹣t2.最后利用点到直线的距离公式列式,采用换元法并且运用基本不等式求最值,即可算出P到直线MN的距离d的最小值为![]() .
.
(1)C1的焦点为![]() ,所以
,所以![]() =0+1,得p=2.故C1的方程为x2=4y,其准线方程为y=-1.
=0+1,得p=2.故C1的方程为x2=4y,其准线方程为y=-1.
(2)设P(2t,t2),M![]() ,N
,N![]() ,则PM的方程为y-
,则PM的方程为y-![]() =x1(x-x1),将P点坐标代入得t2=2tx1-
=x1(x-x1),将P点坐标代入得t2=2tx1-![]() x+1,即x-4tx1+2t2-2=0,同理得x-4tx2+2t2-2=0.MN的方程为y-
x+1,即x-4tx1+2t2-2=0,同理得x-4tx2+2t2-2=0.MN的方程为y-![]() =
=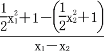 (x-x1),即y-
(x-x1),即y-![]() =
=![]() (x1+x2)(x-x1).
(x1+x2)(x-x1).
由![]() 得x1+x2=4t,
得x1+x2=4t,![]() x-2tx1=1-t2,所以直线MN的方程为y=2tx+2-t2.
x-2tx1=1-t2,所以直线MN的方程为y=2tx+2-t2.
于是d=![]() =2
=2![]() .
.
令s=1+4t2(s≥1),则d=![]()
![]() ≥
≥![]()
![]() =
=![]() (当且仅当s=3时取等号),
(当且仅当s=3时取等号),
所以d的最小值为![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】设k是一个正整数,(1+ ![]() )k的展开式中第四项的系数为
)k的展开式中第四项的系数为 ![]() ,记函数y=x2与y=kx的图象所围成的阴影部分为S,任取x∈[0,4],y∈[0,16],则点(x,y)恰好落在阴影区域内的概率为( )
,记函数y=x2与y=kx的图象所围成的阴影部分为S,任取x∈[0,4],y∈[0,16],则点(x,y)恰好落在阴影区域内的概率为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为  (t为参数),以坐标原点为极点,x轴的非负半轴为极轴,建立极坐标系,圆C的极坐标方程为ρ=4cosθ,直线l与圆C交于A,B两点.
(t为参数),以坐标原点为极点,x轴的非负半轴为极轴,建立极坐标系,圆C的极坐标方程为ρ=4cosθ,直线l与圆C交于A,B两点.
(1)求圆C的直角坐标方程及弦AB的长;
(2)动点P在圆C上(不与A,B重合),试求△ABP的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若
(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若![]() ,
,![]() ,cos ∠ABF=
,cos ∠ABF=![]() ,则C的离心率为( )
,则C的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从边长为2a的正方形铁片的四个角各截去一个边长为x的正方形,然后折成一个无盖的长方体盒子,要求长方体的高度x与底面正方形边长的比不超过正数t.
(1)把铁盒的容积V表示为关于x的函数,并指出其定义域.
(2)当x为何值时,容积V有最大值?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=3sinx﹣πx,命题p:x∈(0, ![]() ),f(x)<0,则( )
),f(x)<0,则( )
A.p是假命题,¬p:?x∈(0, ![]() ),f(x)≥0
),f(x)≥0
B.p是假命题,¬p:?x0∈(0, ![]() ),f(x0)≥0
),f(x0)≥0
C.p是真命题,¬p:?x∈(0, ![]() ),f(x)>0
),f(x)>0
D.p是真命题,¬p:?x0∈(0, ![]() ),f(x0)≥0
),f(x0)≥0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln x-mx+n,m,n∈R.
(1)若函数f(x)的图像在点(1,f(1))处的切线为y=2x-1,求m,n的值;
(2)求函数f(x)的单调区间;
(3)若n=0,不等式f(x)+m<0对x∈(1,+∞)恒成立,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com