
【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x﹣2)2+(y﹣3)2=1交于点M,N两点.
(1)求k的取值范围;
(2)请问是否存在实数k使得 ![]() (其中O为坐标原点),如果存在请求出k的值,并求|MN|;如果不存在,请说明理由.
(其中O为坐标原点),如果存在请求出k的值,并求|MN|;如果不存在,请说明理由.
【答案】
(1)解:由题设,可知直线l的方程为y=kx+1,因为直线l与圆C交于两点,
由已知可得圆C的圆心C的坐标(2,3),半径R=1.
故由 ![]() <1,解得:
<1,解得: ![]() <k<
<k< ![]()
所以k的取值范围为得( ![]() ,
, ![]() )
)
(2)解:设M(x1,y1),N(x2,y2).
将y=kx+1代入方程:(x﹣2)2+(y﹣3)2=1,
整理得(1+k2)x2﹣4(1+k)x+7=0.
所以x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
![]()
![]() =x1x2+y1y2=(1+k2)(x1x2)+k(x1+x2)+1=
=x1x2+y1y2=(1+k2)(x1x2)+k(x1+x2)+1= ![]() =12,
=12,
解得k=1,所以直线l的方程为y=x+1.
故圆心C在直线l上,所以|MN|=2.
【解析】(1)设出直线方程,利用直线与圆的位置关系,列出不等式求解即可.(2)设出M,N的坐标,利用直线与圆的方程联立,通过韦达定理,结合向量的数量积,求出直线的斜率,然后判断直线与圆的位置关系求解|MN|即可.
【考点精析】本题主要考查了直线与圆的三种位置关系的相关知识点,需要掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点才能正确解答此题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】医学上所说的“三高”通常是指血脂增高、血压增高、血糖增高等疾病.为了解“三高”疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:
(1)请将列联表补充完整;
患三高疾病 | 不患三高疾病 | 合计 | |
男 | 6 | 30 | |
女 | |||
合计 | 36 |
(2)能否在犯错误的概率不超过0.005的前提下认为患“三高”疾病与性别有关? 下列的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=2,an+1=2﹣ ![]() (n=1,2,3,…).
(n=1,2,3,…).
(Ⅰ)求a2 , a3 , a4的值,猜想出数列的通项公式an;
(Ⅱ)用数学归纳法证明你的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数 ![]() 的图象上所有点的横坐标变为原来的2倍(纵坐标不变),再把所得图象上所有点向左平移
的图象上所有点的横坐标变为原来的2倍(纵坐标不变),再把所得图象上所有点向左平移 ![]() 个单位长度,得到图象的函数解析式为( )
个单位长度,得到图象的函数解析式为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“描点法”画函数![]() 在区间
在区间![]() 上的图象时,列表并填入了部分数据,如下表:
上的图象时,列表并填入了部分数据,如下表:

(1)请将上表数据补充完整,并在给出的直角坐标系中,画出![]() 在区间
在区间![]() 上的图象;
上的图象;
(2)利用函数的图象,直接写出函数![]() 在
在![]() 上的单调递增区间;
上的单调递增区间;

(3)将![]() 图象上所有点向左平移
图象上所有点向左平移![]() 个单位长度,得到
个单位长度,得到![]() 的图象,若
的图象,若
![]() 图象的一个对称中心为
图象的一个对称中心为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥V-ABC中,平面VAB![]() 平面ABC,
平面ABC, ![]() VAB为等边三角形,AC
VAB为等边三角形,AC![]() BC且AC=BC=
BC且AC=BC=![]() ,O,M分别为AB,VA的中点。
,O,M分别为AB,VA的中点。
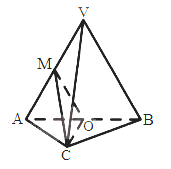
(I)求证:VB//平面MOC;
(II)求证:平面MOC![]() 平面VAB;
平面VAB;
(III)求三棱锥V-ABC的体积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com